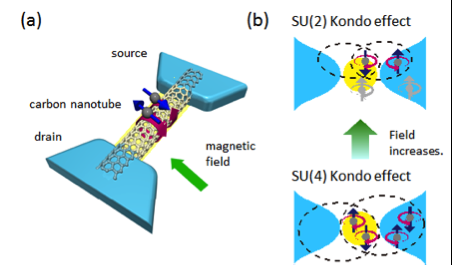
Figura 1:(a) I gradi di libertà di spin e orbitali dell'elettrone in un punto quantico di nanotubi di carbonio sono mostrati dalle frecce blu diritte e dalle frecce viola circolari, rispettivamente. Possiamo controllare il numero di elettroni nel punto quantico uno per uno dall'elettrodo di gate vicino (non mostrato in figura). (b) A causa dello spin e dei gradi di libertà orbitali, uno stato SU(4) Kondo si forma a campo magnetico zero come mostrato nel pannello inferiore. Ad alto campo magnetico evolve continuamente in un effetto SU(2) Kondo (pannello superiore). Credito:Università di Osaka
Le transizioni di fase includono fenomeni comuni come il congelamento o l'ebollizione dell'acqua. Allo stesso modo, anche i sistemi quantistici a una temperatura dello zero assoluto sperimentano transizioni di fase. La pressione o il campo magnetico applicato a tali sistemi può essere regolato in modo che questi sistemi arrivino a un punto di non ritorno tra due fasi. A questo punto fluttuazioni quantistiche, piuttosto che sbalzi di temperatura, guidare queste transizioni.
Molti fenomeni affascinanti con applicazioni tecnologiche promettenti in aree come la superconduttività sono legati alle transizioni di fase quantistiche, ma il ruolo delle fluttuazioni quantistiche in tali transizioni rimane poco chiaro. Sebbene ci siano stati molti progressi nella comprensione del comportamento di singole particelle come i protoni, neutroni, e fotoni, la sfida di comprendere sistemi contenenti molte particelle che interagiscono fortemente tra loro deve ancora essere risolta.
Ora, un team di ricerca internazionale guidato da un gruppo dell'Università di Osaka ha scoperto un chiaro legame tra le fluttuazioni quantistiche e la carica effettiva delle particelle che trasportano corrente. Questa scoperta aiuterà i ricercatori a scoprire come le fluttuazioni quantistiche governano i sistemi in cui interagiscono molte particelle. Un esempio di un tale sistema è l'interazione degli elettroni a temperature estremamente basse. Mentre le basse temperature normalmente fanno diminuire la resistenza in un metallo, la resistenza aumenta di nuovo a temperature estremamente basse a causa di piccole impurità magnetiche, questo è indicato come effetto Kondo.
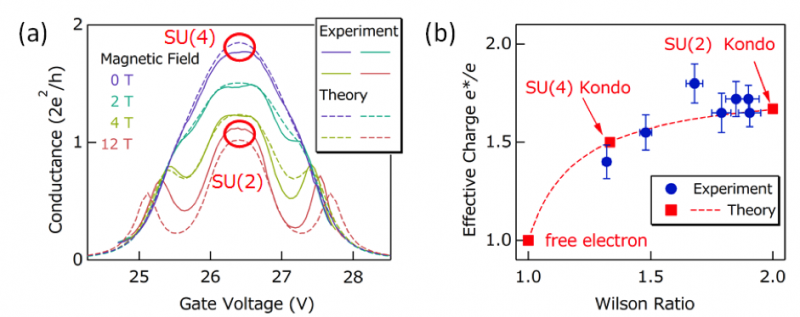
Figura 2:(a) Conduttanza del punto quantico in funzione della tensione di gate. La conduttanza è normalizzata dal quanto di conduttanza (2e2/h). I dati sperimentali (linee continue) ei risultati dei calcoli del gruppo di rinormalizzazione numerica (NRG) (linee tratteggiate) sono quantitativamente coerenti tra loro. (b) I cerchi pieni mostrano la carica effettiva e*/e in funzione del rapporto di Wilson che quantifica la forza delle fluttuazioni. La carica effettiva e*/e è derivata dal rumore di corrente e il rapporto di Wilson rappresenta le fluttuazioni quantistiche. Tre simboli quadrati rappresentano la previsione teorica per SU(4), SU(2), e particelle non interagenti. La linea tratteggiata è la previsione teorica estesa, che collega bene il crossover di simmetria degli stati fondamentali liquidi quantistici. Credito:Università di Osaka
"Abbiamo usato un campo magnetico per sintonizzare lo stato di Kondo in un nanotubo di carbonio, assicurando che le fluttuazioni quantistiche fossero l'unica variabile nel sistema, ", afferma il coautore dello studio Kensuke Kobayashi. "Monitorando direttamente la conduttanza e il rumore di sparo del nanotubo di carbonio, siamo stati in grado di dimostrare un continuo crossover tra gli stati di Kondo con diverse simmetrie."
Utilizzando questo nuovo approccio, i ricercatori hanno scoperto un legame tra le fluttuazioni quantistiche e la carica effettiva delle particelle che trasportano corrente, e*. La scoperta significa che le misurazioni di e* possono essere utilizzate per quantificare le fluttuazioni quantistiche.
"Questo è molto eccitante, poiché apre la strada a future indagini sull'esatto ruolo delle fluttuazioni quantistiche nelle transizioni di fase quantistiche, " spiega il professor Kobayashi. Comprendere le transizioni di fase quantistiche ha il potenziale per consentire molte applicazioni interessanti in aree come la superconduttività, Isolatori Mott, e l'effetto Hall quantistico frazionario.