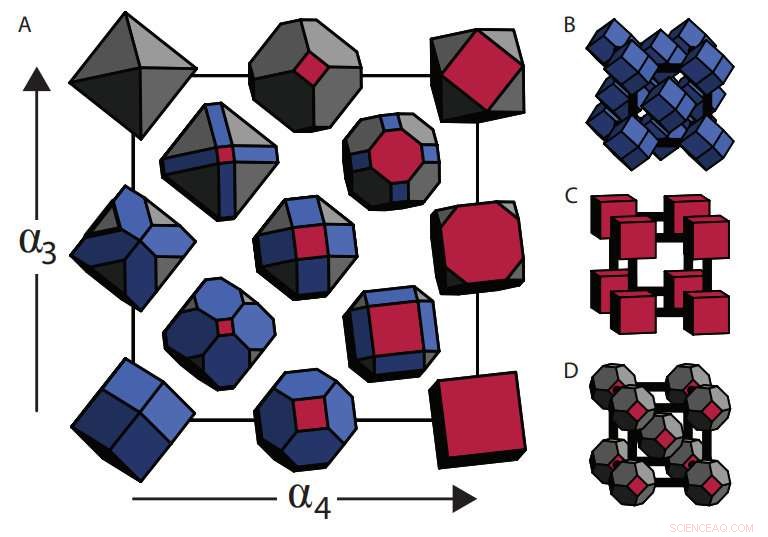
Famiglia di forme e strutture. Gli autori si basano su una parametrizzazione precedentemente definita (A) che mappa continuamente due valori, α3 e α4, a poliedri convessi. Questa parametrizzazione, qui conosciuto come ∆ 423 famiglia, contiene le forme di riempimento dello spazio per (B) FCC, (C) SC e (D) BCC. Credito:Rose Cersonsky et al., arXiv:1712.02473 [cond-mat.soft]
Le forme tridimensionali riempiono lo spazio fisico in un certo modo. Se versi delle biglie in un barattolo, le biglie si impacchettano casualmente all'interno del barattolo. Se hai posizionato con cura ogni marmo, strato per strato nel barattolo in modo che le biglie in uno strato si trovino nelle fessure tra le biglie sullo strato sottostante, puoi mettere qualche biglia in più nel barattolo rispetto a se fosse confezionato a caso. Questo ti darà la più alta densità di imballaggio, o la minima quantità di spazio tra le particelle.
Linus Pauling ha applicato questa idea di densità di impacchettamento agli ioni, e propose che i principi di impaccamento portassero alla formazione di strutture cristalline. La natura non ama lo spazio vuoto, quindi le particelle dovrebbero impacchettarsi nella più alta densità o in una formazione compatta. Nel campo della scienza dei materiali, cristalli colloidali e superreticoli di nanoparticelle si formano tramite l'autoassemblaggio di piccole particelle in cui le particelle formano una struttura termodinamicamente stabile. Le strutture che si formano le nanoparticelle sono molto spesso quelle che si trovano nei metalli convenzionali:cubiche a facce centrate, cubico semplice, e cubica a corpo centrato.
La teoria è che i principi dell'impaccamento guidano l'autoassemblaggio dei cristalli colloidali. Però, ricercatori dell'Università del Michigan hanno dimostrato che il meccanismo di ordinamento per i cristalli colloidali non lo fa causa particelle da autoassemblare. Invece l'assemblaggio e l'imballaggio dei cristalli sono correlati, non causale. Per di più, mostrano che i principi di impaccamento potrebbero non essere il miglior strumento di previsione per la forma del cristallo colloidale. Il loro lavoro appare in Gli Atti dell'Accademia Nazionale delle Scienze .
Nell'autoassemblaggio, si forma una struttura termodinamicamente stabile. Questa struttura riduce al minimo l'energia libera. Per i colloidi, questo accade spesso quando l'entropia è al massimo. Però, nello studio dei meccanismi che guidano l'autoassemblaggio, i ricercatori osservano cosa succede in condizioni estreme. A pressioni molto elevate, invece di massimizzare l'entropia, le particelle dure massimizzeranno la densità.
Per indagare sulla questione fondamentale se i principi di imballaggio guidano l'autoassemblaggio, Cersonsky, et al. metodi di modellazione utilizzati per confrontare tre diversi termini di densità. Il primo è la densità di autoassemblaggio, che è la densità più bassa in cui si osserva l'autoassemblaggio. Il secondo è l'impaccamento della densità di insorgenza. Come il nome suggerisce, questa è la densità più bassa in cui si osserva il comportamento di impacchettamento. Il terzo termine è la densità di impacchettamento casuale ravvicinata, che è la densità massima che il sistema può trovare in uno stato disordinato.
Quando si osservano modelli matematici a pressioni molto elevate (cioè, pressione infinita), dovrebbe esserci un confine in corrispondenza del quale le particelle devono essere impacchettate. Gli autori hanno testato questo confine utilizzando le relazioni di Maxwell per definire la densità di inizio dell'impaccamento. Se si trova che la densità di autoassemblaggio è approssimativamente uguale alla densità di inizio dell'imballaggio, quindi è probabile che l'imballaggio guidi l'autoassemblaggio. Però, se la densità di autoassemblaggio è inferiore alla densità di imballaggio, quindi qualcosa di diverso dalle regole di imballaggio guida l'autoassemblaggio. Per di più, la densità di impaccamento viene confrontata con la densità di impaccamento casuale.
Cersonsky et al. trovato che in tutti i sistemi poliedrici che hanno studiato (FCC, NS, e BCC) la densità di impaccamento era maggiore della densità di impaccamento ravvicinato casuale, che era maggiore della densità minima per l'autoassemblaggio. Questo risultato mostra che l'ordine spontaneo non si verifica a causa di un meccanismo di imballaggio e che questi sistemi non possono essere ordinati tramite imballaggio. In altre parole, le regole di imballaggio non sono necessariamente predittive delle forme ideali per l'autoassemblaggio anche se la struttura di imballaggio densa è la struttura termodinamicamente più stabile.
Questo documento ha esaminato le nanoparticelle che non erano confinate. Secondo Greg van Anders, assistente professore di fisica e coautore del documento, "Ci aspettavamo di scoprire che i colloidi avrebbero ordinato imballando. Invece, abbiamo scoperto che non lo fanno. Ciò è particolarmente sorprendente perché le particelle non si impacchettano anche quando le strutture che formano sono le cosiddette strutture "ravvicinate".
Di solito nella scienza dei materiali, le regole di imballaggio vengono utilizzate per prevedere la forma ottimale per una nanostruttura, ma visti questi risultati, la domanda diventa se, e quando, le regole di imballaggio possono essere utilizzate per prevedere la forma termodinamicamente ottimale per l'autoassemblaggio.
C'è ancora una certa correlazione tra la forma dell'imballaggio e la forma ottimale delle particelle, e quindi, la forma dell'imballaggio può essere utile per guidare le previsioni, ma le forme di imballaggio ideali non dovrebbero essere l'obiettivo nell'assemblaggio di nanostrutture. Il Dr. van Anders sottolinea che questa è in realtà una buona notizia per le persone che cercano di sintetizzare nanoparticelle poliedriche che si autoassemblano in nanostrutture:
"Dopo aver scoperto che il meccanismo che guida la formazione della struttura non è l'impaccamento, ci siamo resi conto che questo potrebbe significare che particelle dalla forma perfetta, che imballano più densamente, ma può essere tecnicamente impegnativo e costoso da realizzare, potrebbe non essere la forma ideale per le strutture target."
© 2018 Phys.org