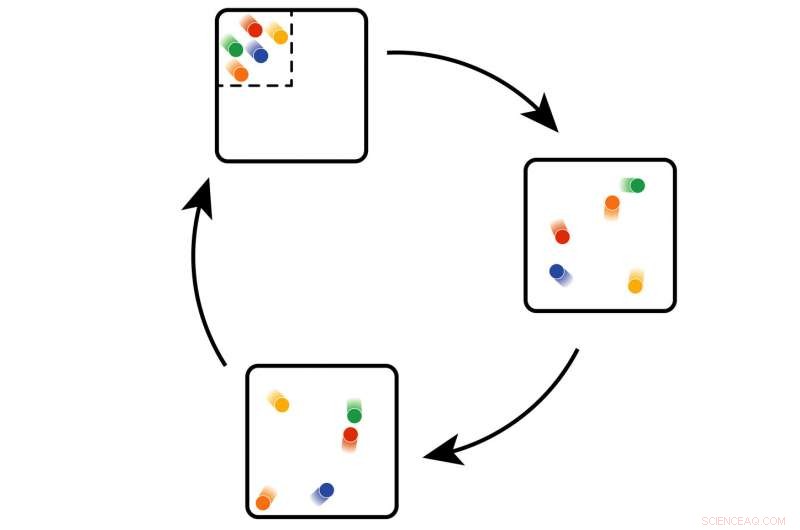
La ricorrenza può essere dimostrata con le palline in una scatola:quando iniziano in uno stato ordinato, diventeranno più disordinati. Ma a un certo punto, torneranno allo stato iniziale -- potrebbe volerci del tempo. Attestazione:TU Wien
È uno dei risultati più sorprendenti della fisica:quando un sistema complesso viene lasciato solo, tornerà al suo stato iniziale con una precisione quasi perfetta. Particelle di gas, Per esempio, vorticando caoticamente in un contenitore, ritorneranno quasi esattamente alle loro posizioni di partenza dopo un po' di tempo. Il teorema della ricorrenza di Poincaré è il fondamento della moderna teoria del caos. Per decenni, gli scienziati hanno studiato come questo teorema può essere applicato al mondo della fisica quantistica. Ora, i ricercatori della TU Wien (Vienna) hanno dimostrato con successo una sorta di ricorrenza di Poincaré in un sistema quantistico multiparticellare. I risultati sono stati pubblicati sulla rivista Scienza .
Alla fine del XIX secolo, lo scienziato francese Henri Poincaré ha studiato sistemi che non possono essere analizzati completamente con precisione perfetta, ad esempio, sistemi solari costituiti da molti pianeti e asteroidi, o particelle di gas che continuano a urtarsi l'una contro l'altra. Il suo risultato sorprendente:ogni stato fisicamente possibile sarà occupato dal sistema ad un certo punto, almeno con un ottimo grado di approssimazione. Se aspettiamo abbastanza a lungo, ad un certo punto tutti i pianeti formeranno una linea retta, solo per coincidenza. Le particelle di gas in una scatola creeranno modelli interessanti, o tornare allo stato in cui si trovavano all'inizio dell'esperimento.
Un teorema simile può essere dimostrato per i sistemi quantistici. Là, però, si applicano regole completamente diverse:"Nella fisica quantistica, dobbiamo trovare un modo completamente nuovo di affrontare questo problema, " afferma il professor Jörg Schmiedmayer dell'Istituto di fisica atomica e subatomica della TU Wien. "Per ragioni fondamentali, lo stato di un grande sistema quantistico, costituito da molte particelle, non può mai essere misurato perfettamente. A parte quello, le particelle non possono essere viste come oggetti indipendenti, dobbiamo tener conto del fatto che sono quantisticamente entangled."

Il chip atomico, utilizzato per controllare le nuvole atomiche ultra fredde. Attestazione:TU Wien
Ci sono stati tentativi di dimostrare l'effetto della "ricorrenza di Poincaré" nei sistemi quantistici, ma fino ad ora questo è stato possibile solo con un numero molto piccolo di particelle, il cui stato è stato misurato nel modo più preciso possibile. Questo è estremamente complicato e il tempo necessario al sistema per tornare al suo stato originale aumenta notevolmente con il numero di particelle. Il team di Jörg Schmiedmayers alla TU Wien, però, ha scelto un approccio diverso:"Non siamo tanto interessati allo stato interno completo del sistema, che comunque non può essere misurato, "dice Bernhard Rauer, primo autore della pubblicazione. "Vogliamo invece chiederci:quali grandezze possiamo osservare, che ci dicono qualcosa di interessante sul sistema nel suo insieme? E ci sono momenti in cui queste quantità collettive tornano al loro valore iniziale?"
Il team ha studiato il comportamento di un gas ultrafreddo, composto da migliaia di atomi, che viene mantenuto in posizione da campi elettromagnetici su un chip. "Ci sono diverse quantità che descrivono le caratteristiche di un tale gas quantistico, ad esempio lunghezze di coerenza nel gas e funzioni di correlazione tra diversi punti nello spazio. Questi parametri ci dicono, quanto strettamente le particelle sono collegate da effetti della meccanica quantistica, "dice Sebastian Erne, che era responsabile dei calcoli teorici necessari per il progetto. "La nostra intuizione quotidiana non è abituata a trattare queste quantità, ma per un sistema quantistico, sono fondamentali".
Ricorrenza scoperta—in quantità collettive
Misurando tali quantità, che non si riferiscono a singole particelle, ma caratterizzano il sistema nel suo insieme, è stato infatti possibile osservare la ricorrenza quantistica a lungo cercata. E non solo:"Con il nostro chip atomico, possiamo persino influenzare il tempo impiegato dal sistema per tornare a uno stato particolare, " dice Jörg Schmiedmayer. "Misurando questo tipo di ricorrenza, impariamo molto sulle dinamiche collettive degli atomi, ad esempio sulla velocità del suono nel gas o sui fenomeni di diffusione delle onde di densità".
La vecchia domanda, se i sistemi quantistici mostrano ricorrenze, si può finalmente rispondere:sì, lo fanno, ma il concetto di ricorrenza deve essere leggermente ridefinito. Invece di cercare di mappare lo stato quantico interno completo di un sistema, che comunque non può essere misurato, ha più senso concentrarsi su quantità che possono essere misurate negli esperimenti quantistici. Si può osservare che queste quantità si allontanano dal loro valore iniziale e alla fine ritornano al loro stato iniziale.