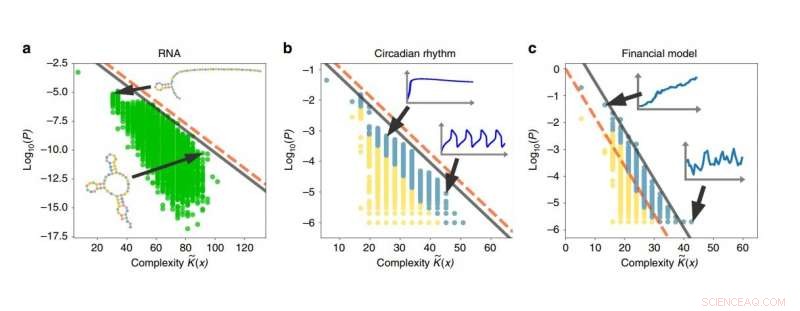
Esempi di bias di semplicità nelle sequenze di RNA, ritmi circadiani, e modelli finanziari. Maggiore è la complessità di un output, minore è la probabilità che l'output venga generato. Credito:Dingle, et al. Pubblicato in Comunicazioni sulla natura
I ricercatori hanno scoperto che le mappe input-output, che sono ampiamente utilizzati in tutta la scienza e l'ingegneria per modellare sistemi che vanno dalla fisica alla finanza, sono fortemente orientati alla produzione di output semplici. I risultati sono sorprendenti, poiché ingenuamente non c'è motivo di sospettare che un output sia più probabile di un altro.
I ricercatori, Kamaludin Dingle, Chico Q. Camargo, e Ard A. Louis, all'Università di Oxford e alla Gulf University for Science and Technology, hanno pubblicato un articolo sui loro risultati in un recente numero di Comunicazioni sulla natura .
"Il più grande significato del nostro lavoro è la nostra previsione che il bias di semplicità - che è esponenzialmente più probabile che vengano generati output semplici rispetto a output complessi - vale per un'ampia varietà di sistemi scientifici e ingegneristici, "Luigi ha detto Phys.org . "Il bias di semplicità implica che, per un sistema fatto di molte diverse parti interagenti, diciamo, un circuito con molti componenti, una rete con molte reazioni chimiche, ecc.:la maggior parte delle combinazioni di parametri e input dovrebbe portare a un comportamento semplice."
Il lavoro attinge dal campo della teoria dell'informazione algoritmica (AIT), che si occupa delle connessioni tra informatica e teoria dell'informazione. Un importante risultato dell'AIT è il teorema della codifica. Secondo questo teorema, quando una macchina di Turing universale (un dispositivo di calcolo astratto in grado di calcolare qualsiasi funzione) riceve un input casuale, gli output semplici hanno una probabilità esponenzialmente maggiore di essere generati rispetto agli output complessi. Come spiegano i ricercatori, questo risultato è completamente in contrasto con l'ingenua aspettativa che tutti i risultati siano ugualmente probabili.
Nonostante questi interessanti risultati, finora il teorema di codifica è stato applicato raramente a qualsiasi sistema del mondo reale. Questo perché il teorema è stato formulato solo in modo molto astratto, e una delle sue componenti chiave, una misura di complessità chiamata complessità di Kolmogorov, non è calcolabile.
"Il teorema di codifica di Solomonoff e Levin è un risultato notevole che dovrebbe essere conosciuto molto più ampiamente, "Ha detto Louis. "Si prevede che gli output a bassa complessità siano esponenzialmente più probabilità di essere generati da una macchina di Turing universale (UTM) rispetto agli output ad alta complessità. Poiché tutto ciò che è calcolabile può essere calcolato su un UTM, questa è una previsione piuttosto sorprendente!
"Però, il teorema della codifica è rimasto oscuro perché gli UTM sono piuttosto astratti, perché può essere dimostrato solo nel limite asintotico di grandi complessità, e perché la misura di Kolmogorov utilizzata per determinare la complessità è fondamentalmente non calcolabile. Il nostro lavoro aggira questi problemi utilizzando una versione leggermente più debole del teorema di codifica che è molto più facile da applicare."
Nel nuovo, versione più debole del teorema di codifica, i ricercatori hanno sostituito la complessità di Kolmogorov con una complessità di approssimazione, che è calcolabile, pur conservando la preferenza esponenziale per la semplicità. Il teorema di codifica più debole può essere facilmente applicato per fare previsioni su sistemi pratici.
"Usiamo il linguaggio delle mappe input-output, che può sembrare piuttosto astratto, " disse Louis. "Tuttavia, molti sistemi studiati in scienze e ingegneria convertono un qualche tipo di input in qualche tipo di output attraverso un algoritmo. Per esempio, le informazioni codificate nel DNA di un organismo (il suo genotipo) potrebbero essere viste come input, mentre le caratteristiche e il comportamento dell'organismo (il suo fenotipo) potrebbero essere visti come l'output. In un insieme di equazioni differenziali, l'input sono i parametri delle equazioni, e l'output è la soluzione di tali equazioni, date alcune condizioni al contorno.
"Noi sosteniamo che se scegli casualmente i parametri di input, allora è esponenzialmente più probabile che tali sistemi producano output semplici rispetto a output complessi. Poiché questa previsione vale per un'ampia gamma di mappe, stiamo facendo un'ampia affermazione. Ma questo è uno dei suoi punti di forza. La nostra derivazione non richiede di sapere molto su come funziona effettivamente la mappa (o l'algoritmo) in questione.
"Quindi il significato principale del nostro lavoro è che la nostra versione più debole del teorema di codifica mantiene approssimativamente la tendenza esponenziale verso la semplicità del teorema di codifica originale, ma è molto più facile da applicare nella pratica."
Una conseguenza dei risultati è che è possibile prevedere la probabilità di un particolare risultato in base alla sua complessità. Sebbene sia esponenzialmente più probabile che appaia un output semplice rispetto a un output complesso, i ricercatori osservano che ciò non significa necessariamente che gli output semplici abbiano maggiori probabilità di apparire rispetto agli output complessi in generale, poiché potrebbero esserci molti output più complessi di quelli semplici nel complesso.
Per illustrare alcune applicazioni, i ricercatori hanno utilizzato il teorema di codifica modificato per analizzare sistemi di sequenze di RNA, ritmi circadiani, e mercati finanziari, e ha mostrato che tutti questi sistemi mostrano il bias di semplicità. Nel futuro, hanno anche in programma di applicare i risultati ad algoritmi informatici, evoluzione biologica, e sistemi caotici. Però, per una spiegazione più intuitiva di cosa significhi bias di semplicità, i ricercatori descrivono uno scenario che coinvolge i nostri parenti primati:
"Si consideri il noto problema delle scimmie che digitano su una macchina da scrivere, " disse Louis. "Se le scimmie digitano in modo davvero casuale, e la macchina da scrivere ha n chiavi, quindi la probabilità di ottenere una particolare sequenza di lunghezza K è solo 1/ n K , poiché c'è un 1/ n possibilità di ottenere la giusta sequenza di tasti in ciascuna delle K passi. Quindi ogni sequenza di lunghezza K è ugualmente probabile o improbabile.
"Ora considera il caso in cui le scimmie stanno digitando in un programma per computer. Possono quindi digitare per sbaglio un programma breve che genera un output lungo. Ad esempio, esiste un codice di 133 caratteri nel linguaggio di programmazione C che genera correttamente i primi 15, 000 cifre di . Quindi invece di 1/ n 15, 000 , che è la probabilità che le scimmie riescano a farlo bene su una macchina da scrivere, le probabilità sono molto più basse, solo 1/ n 133 , che le scimmie generano sul computer.
Si scopre che la maggior parte dei numeri non ha programmi brevi che li generano, quindi il meglio che le scimmie sul computer possono fare per questi numeri è digitare un programma come "stampa numero, ' che è vicina alla probabilità che lo farebbero comunque bene su una macchina da scrivere. Ma per output semplici, la probabilità è molto più alta che per la macchina da scrivere. Per definizione, output semplici sono definiti come quelli che hanno brevi programmi che li descrivono, e gli output complessi sono quelli che possono essere descritti solo da programmi lunghi. Quindi π è, per definizione, un numero a bassa complessità, e quindi è molto più probabile che sia generato da scimmie che digitano in un programma per computer rispetto a molti altri numeri che non sono semplici.
"Ciò che fa il teorema della codifica è rendere quantitativa questa storia intuitiva. È più probabile che i programmi brevi vengano digitati a caso, e poiché le probabilità per la lunghezza K i programmi scalano anche come 1/ n K , gli output semplici sono esponenzialmente molto più probabili di quelli complessi. Il nostro contributo è dimostrare come calcolare facilmente la relazione esponenziale tra probabilità e complessità per molti sistemi pratici. La cosa bella è che non è necessario sapere molto sulla mappa (o equivalentemente sull'algoritmo) per capire se è probabile che un output appaia o meno. In buona prima approssimazione, più un output è comprimibile, più è probabile che appaia su input casuali."
© 2018 Phys.org