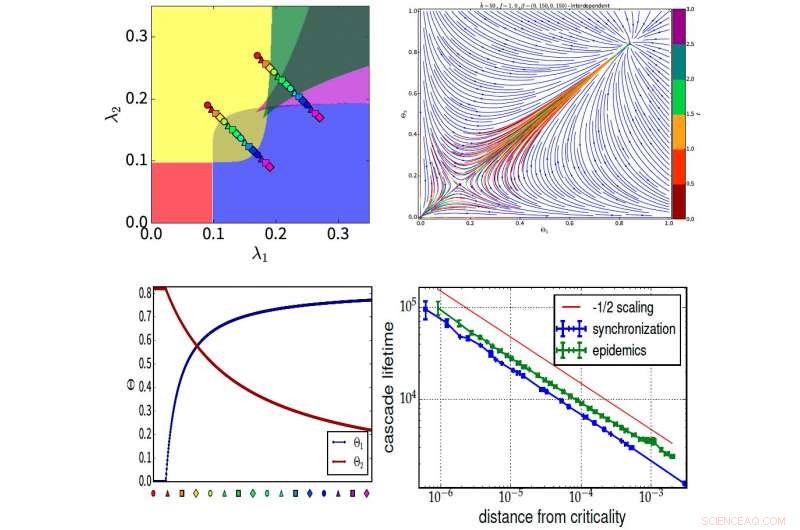
In un articolo pubblicato di recente in Fisica della natura , Università Bar-Ilan Prof. Havlin, e un team di ricercatori, tra cui Stefano Boccaletti, Ivan Bonamassa, e Michael M. Danziger, presentare un quadro di dipendenza dinamica in grado di catturare interazioni interdipendenti e competitive tra sistemi dinamici che vengono utilizzati per studiare i processi di sincronizzazione e diffusione in reti multistrato con strati interagenti. Principali risultati in questa immagine. (In alto a sinistra) Diagramma di fase per due modelli Kuramoto parzialmente competitivi con regioni di multistabilità. (In alto a destra) Risultati teorici e numerici per il flusso di epidemie di SIS interdipendenti (grafici di Erdos-Renyi, grado medio
Molti sistemi complessi del mondo reale includono sottosistemi macroscopici che si influenzano a vicenda. Questo sorge, Per esempio, in popolazioni neurali in competizione o che si rafforzano reciprocamente nel cervello, dinamiche di diffusione dei virus, e altrove. È quindi importante capire come i diversi tipi di interazioni tra sistemi possono influenzare i comportamenti collettivi complessivi.
Nel 2010 sono stati compiuti progressi sostanziali quando la teoria della percolazione su reti interdipendenti è stata introdotta dal Prof. Shlomo Havlin e da un team di ricercatori del Dipartimento di Fisica dell'Università Bar-Ilan in uno studio pubblicato su Natura . Questo modello ha mostrato che quando i nodi di una rete dipendono dai nodi di un'altra per funzionare, sorgono catastrofiche cascate di fallimenti e brusche transizioni strutturali, come è stato osservato nel blackout elettrico che ha interessato gran parte dell'Italia nel 2003.
Percolazione interdipendente, però, è limitato ai sistemi in cui la funzionalità è determinata esclusivamente dalla connettività, fornendo così una comprensione solo parziale di una ricchezza di sistemi del mondo reale la cui funzionalità è definita secondo regole dinamiche.
La ricerca ha dimostrato che due modi fondamentali in cui i nodi in un sistema possono influenzare i nodi in un altro sono l'interdipendenza (o cooperazione), come nelle infrastrutture critiche o nelle reti finanziarie, e antagonismo (o competizione), come osservato nei sistemi ecologici, social networks, o nel cervello umano. Interazioni interdipendenti e competitive possono anche verificarsi simultaneamente, come osservato nelle relazioni predatore-preda nei sistemi ecologici, e nella rivalità binoculare nel cervello.
In un articolo pubblicato di recente in Fisica della natura , Università Bar-Ilan Prof. Havlin, e un team di ricercatori, tra cui Stefano Boccaletti, Ivan Bonamassa, e Michael M. Danziger, presentare un quadro di dipendenza dinamica in grado di catturare interazioni interdipendenti e competitive tra sistemi dinamici che vengono utilizzati per studiare i processi di sincronizzazione e diffusione in reti multistrato con strati interagenti.
"Questo quadro di dipendenza dinamica fornisce un potente strumento per comprendere meglio molti dei sistemi complessi interagenti che ci circondano, " ha scritto Havlin e team. "La generalizzazione delle interazioni dipendenti dalla percolazione ai sistemi dinamici consente lo sviluppo di nuovi modelli per neurali, sistemi sociali e tecnologici che catturano meglio i modi sottili in cui i diversi sistemi possono influenzarsi a vicenda".
La ricerca del Prof. Havlin dal 2000 ha prodotto nuovi metodi matematici innovativi nella scienza delle reti che hanno portato a un'ampia ricerca interdisciplinare nel campo. Dopo la pubblicazione di Havlin e dei suoi colleghi della teoria della percolazione, ha ricevuto il Premio Lilienfeld dell'American Physical Society, che viene assegnato per "un contributo più eccezionale alla fisica". All'inizio di quest'anno ha ricevuto il Premio Israele in Chimica e Fisica.