
Interazioni di onde di solitoni in acque poco profonde. Credito:Liron Barakiva
A volte in acque poco profonde, si può formare un tipo di onda molto più stabile delle onde ordinarie. Chiamati solitoni, questi fenomeni emergono come onde solitarie e possono percorrere lunghe distanze mantenendo la loro forma e velocità, anche dopo essersi scontrati con altre onde.
Però, in alcuni casi le collisioni solitoniche possono generare schemi d'onda complicati, a volte chiamate "onde alfabetiche" poiché assomigliano alle lettere X, si, e H, così come le combinazioni di queste forme. Le onde solitarie e i loro schemi di collisione hanno affascinato gli scienziati sin da quando sono state scoperte nel 19 ns secolo.
Ora in un nuovo studio, i ricercatori hanno scoperto che questi stessi schemi nelle onde d'acqua emergono anche nelle collisioni di solitoni ottici (onde luminose con le stesse proprietà stabili). I ricercatori mostrano che la stessa equazione, chiamata equazione di Kadomtsev-Petviashvili II (KPII), che viene utilizzato per modellare le interazioni solitoni dell'acqua può essere utilizzato anche per modellare interazioni solitoni ottici, rivelando una stretta connessione tra la dinamica ondulatoria dell'acqua e della luce.
Teodoro P. Horikis, presso il Dipartimento di Matematica, Università di Giannina, e Dimitrios J. Frantzeskakis, presso il Dipartimento di Fisica, Università di Atene, hanno pubblicato un articolo sui pattern nei solitoni ottici in un recente numero di Atti della Royal Society A .
"Siamo stati tutti su una spiaggia e abbiamo notato gli intricati schemi che le onde formano nell'acqua bassa, vicino alla battigia:bella X-, Y-, e anche le forme d'onda a forma di H emergono spesso dall'interazione di onde diritte, "Horikis ha detto Phys.org . "Sorprendentemente, questi fenomeni sono pienamente compresi e possono essere descritti matematicamente in dettaglio utilizzando modelli matematici appropriati. Tensione superficiale, che è il fenomeno che fa sì che i fluidi riducano al minimo l'area che occupano, svolge un ruolo importante nella formazione di X-, Y-, e onde a forma di H. In acqua, la tensione superficiale è piccola, mentre nel mercurio, Per esempio, la tensione superficiale è grande.
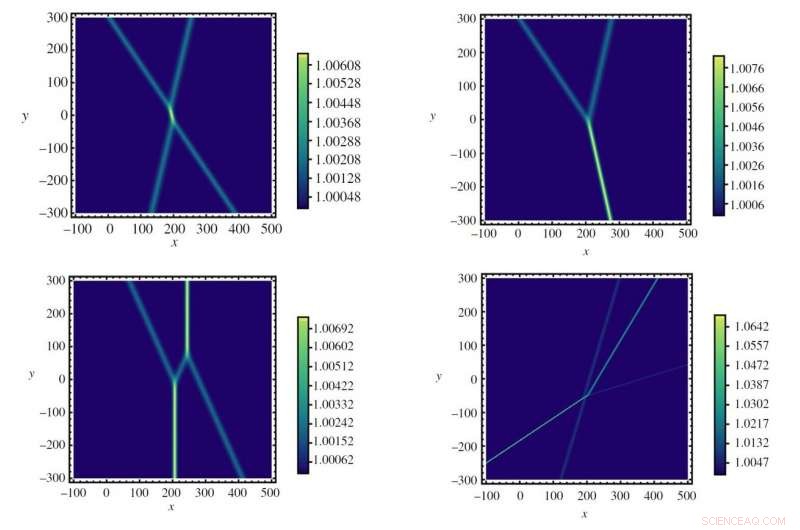
Risultati della simulazione che mostrano diversi modelli che emergono nelle interazioni di solitoni ottici. Credito:Horikis e Frantzeskakis. ©2019 La Società Reale
"Abbiamo dimostrato che la propagazione di solitoni ottici in mezzi non locali, che includono plasmi, cristalli liquidi nematici e soluzioni liquide con non linearità termiche, è governato dallo stesso modello utilizzato per descrivere acque poco profonde, con nonlocalità che gioca il ruolo di tensione superficiale. Così, infatti, 'la luce incontra l'acqua, ' come prevediamo che X-, Y-, a forma di H, e le strutture ondose ancora più complicate che osserviamo nelle spiagge piatte possono essere osservate anche in ottica, come fasci ottici che si propagano in mezzi non lineari non locali."
Come hanno spiegato i ricercatori, un mezzo ottico è non locale quando la sua risposta alla luce dipende non solo dalla posizione in cui viene applicato il campo ottico esterno (come in un mezzo locale), ma anche sulla superficie totale e sul volume del mezzo. Nei media non locali, la luce che colpisce in un certo punto viene trasportata nella regione circostante, in modo che un fascio ottico localizzato stretto possa indurre una risposta spazialmente ampia del mezzo. L'analogia tra la debole tensione superficiale dell'acqua e la forte non località in certi mezzi ottici è ciò che consente la descrizione dei solitoni ottici in termini dell'equazione KPII.
"Ciò che è importante nel nostro articolo è che questi due fenomeni, nonlocalità nell'ottica e tensione superficiale nell'acqua, sembrano avere una corrispondenza biunivoca, per così dire, " ha detto Horikis. "È importante che solitoni ottici che sarebbero instabili in mezzi con non località debole, o in fluidi con forte tensione superficiale (come il mercurio), può diventare stabile in supporti ottici fortemente non locali. A causa di questo importante effetto di stabilizzazione indotto dalla forte nonlocalità, il mezzo ottico ospite può supportare solitoni in modo molto simile alla superficie dell'acqua, il cui contatto con l'aria agisce come un sottile foglio elastico su cui possono formarsi queste 'onde alfabetiche'!"
Sulla base di questo risultato, i ricercatori hanno utilizzato simulazioni numeriche per modellare le collisioni di due o tre solitoni ottici. Simile al caso del solitone dell'acqua, hanno scoperto che X-, Y-, e sono emerse onde a forma di H, e anche che l'angolo dei solitoni interagenti porta a schemi diversi.
I ricercatori si aspettano che possa essere possibile osservare sperimentalmente questi schemi di solitoni ottici utilizzando la tecnologia recentemente utilizzata per osservare i singoli solitoni. Ciò richiederebbe la combinazione di due solitoni all'interno di un mezzo non locale, ad esempio un cristallo liquido nematico, mentre si usano specchi per controllare l'angolo tra i due raggi di luce usati per generare i solitoni.
I loro risultati suggeriscono che in futuro potrebbe anche essere possibile trovare modelli ancora più intricati, come strutture di onde simili a ragnatele, nelle collisioni di solitoni ottici. Hanno anche in programma di indagare se altri sistemi altamente non locali, come i condensati di Bose-Einstein (sistemi quantistici macroscopici composti da atomi ultrafreddi) e i colloidi (miscele contenenti particelle sospese in soluzione), può anche fornire gli ingredienti necessari per sostenere l'emergere di questi modelli.
© 2019 Scienza X Rete