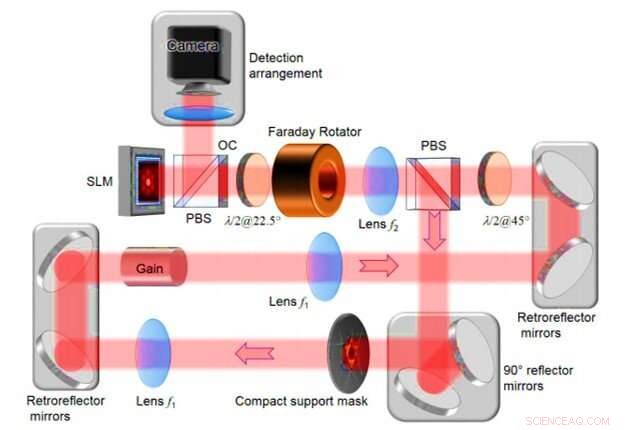
Disposizione laser di cavità degenerata ad anello digitale sperimentale dettagliata. SLM - modulatore di luce spaziale; PBS - divisore di raggio polarizzante; λ/2@22.5° - piastra a semionda con orientamento angolare di 22,5°; λ/2@45° - piastra a semionda con orientamento angolare di 45°; maschera di supporto compatta - apertura intracavità sul piano di Fourier; Accoppiatore uscita OC. Credito:progressi scientifici, doi:10.1126/sciadv.aax4530
I fisici possono esplorare sistemi fisici su misura per risolvere rapidamente compiti computazionali impegnativi sviluppando simulatori di spin, ottimizzazione combinatoria e focalizzazione della luce attraverso mezzi di diffusione. In un nuovo rapporto su Progressi scientifici , C. Tradonsky e un gruppo di ricercatori dei Dipartimenti di Fisica in Israele e in India hanno affrontato il problema del recupero di fase ricostruendo un oggetto dalla sua distribuzione di intensità diffusa. Il processo sperimentale ha affrontato un problema esistente in discipline che vanno dall'imaging a raggi X all'astrofisica che mancano di tecniche per ricostruire un oggetto di interesse, dove gli scienziati usano tipicamente algoritmi iterativi indiretti che sono intrinsecamente lenti.
Nel nuovo approccio ottico, Tradonsky et al hanno invece utilizzato una modalità laser a cavità degenerata digitale (DDCL) per ricostruire in modo rapido ed efficiente l'oggetto di interesse. I risultati sperimentali hanno suggerito che la competizione di guadagno tra le molte modalità laser ha agito come un computer altamente parallelo per dissolvere rapidamente il problema del recupero di fase. L'approccio si applica a oggetti bidimensionali (2-D) con supporto compatto noto e oggetti a valori complessi, generalizzare l'imaging attraverso mezzi di diffusione, mentre si eseguono altri compiti computazionali impegnativi.
Per calcolare relativamente facilmente la distribuzione dell'intensità della luce diffusa lontano da un oggetto sconosciuto, i ricercatori possono calcolare la fonte del valore assoluto della trasformata di Fourier di un oggetto. La ricostruzione di un oggetto dalla sua distribuzione di intensità diffusa è, però, mal posato, poiché le informazioni di fase possono essere perse e diverse distribuzioni di fase nel lavoro possono comportare ricostruzioni diverse. Gli scienziati devono quindi ottenere informazioni preliminari sulla forma di un oggetto, positività, simmetria spaziale o scarsità per ricostruzioni di oggetti più precise. Tali esempi si trovano in astronomia, studi di caratterizzazione a breve impulso, Diffrazione di raggi X, rilevamento radar, riconoscimento vocale e durante l'imaging su supporti torbidi. Durante la ricostruzione di oggetti di estensione finita (supporto compatto), i ricercatori offrono una soluzione unica al problema del recupero di fase, purché modellino la stessa intensità diffusa a una risoluzione sufficientemente più alta.
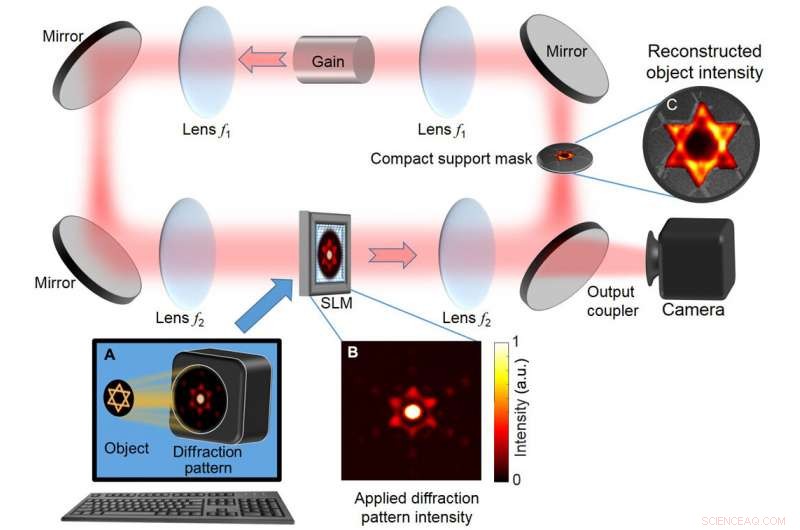
Disposizione DDCL di base per il recupero rapido della fase. (A) La distribuzione dell'intensità diffusa calcolata dall'oggetto (essenzialmente la distribuzione dell'intensità di Fourier) viene applicata su un SLM, che è incorporato in un laser a cavità degenerata ad anello che può supportare fino a 100, 000 modi trasversali degenerati. Una maschera modellata come i confini dell'oggetto (supporto compatto) sul piano di Fourier filtra i modi estranei che non corrispondono al supporto compatto. Con questa disposizione laser, il processo laser produce una soluzione autoconsistente che soddisfa sia la distribuzione di intensità diffusa mostrata in (B) sia il vincolo di supporto compatto. (C) L'intensità dell'oggetto ricostruito appare nella maschera di supporto compatta e viene ripresa sulla fotocamera. a.u., unità arbitrarie. Credito:progressi scientifici, doi:10.1126/sciadv.aax4530
I fisici hanno sviluppato diversi algoritmi per risolvere il problema del recupero di fase nell'ultimo decennio, compreso l'algoritmo di riduzione degli errori di Gerchberg-Saxton (GS), algoritmo ibrido input-input e riflessioni alternate mediate rilassate (RAAR). Però, si basano su proiezioni iterative relativamente lente anche su computer ad alte prestazioni. In alternativa, i team di ricerca possono affrontare le sfide computazionali utilizzando sistemi fisici su misura. Sebbene tali sistemi non siano macchine di Turing universali (cioè, non possono eseguire calcoli arbitrari), possono potenzialmente risolvere una classe specifica di problemi in modo efficiente. Risolvere problemi difficili con tali sistemi può essere vantaggioso rispetto all'uso di computer convenzionali.
Tradonsky et al hanno dimostrato sperimentalmente un nuovo sistema ottico per risolvere rapidamente problemi di recupero di fase basato su un laser a cavità degenerata digitale (DDCL). Il dispositivo incorporava due vincoli, comprese le magnitudini di Fourier della luce diffusa da un oggetto e il supporto compatto. Il processo laser non lineare all'interno della cavità ha portato a una soluzione autoconsistente che ha soddisfatto entrambi i vincoli. Il meccanismo fisico sottostante nel DDCL era simile a quello osservato con gli stimolatori di spin dell'oscillatore parametrico ottico (OPO).
Sia i simulatori OPO che i DDCL hanno eseguito ottimizzazioni tramite operazioni estremamente veloci con la capacità di evitare i minimi locali e possedevano un pacchetto d'onda non gaussiano. Gli scienziati hanno facilitato l'apertura del supporto compatto all'interno della cavità per garantire diverse configurazioni delle fasi laser per provocare perdite diverse, per consentire alla configurazione con perdite minime di vincere la competizione di modalità e risolvere il problema della fase. Il sistema DDCL conteneva molte caratteristiche interessanti e importanti tra cui un elevato parallelismo per fornire milioni di realizzazioni sperimentali parallele, tempi di andata e ritorno brevi di circa 20 nanosecondi, tempi di convergenza rapidi e una modalità di selezione intrinseca che ha rappresentato una perdita minima a causa della modalità di concorrenza. In teoria, di tutte le configurazioni di fase in evoluzione nel tempo, quello con l'energia più alta ha vinto la competizione di modalità relativa al guadagno limitato. Di conseguenza, maggiore il numero di configurazioni indipendenti iniziali in pratica, maggiore è la probabilità che il sistema trovi una soluzione corretta con una configurazione stabile e senza perdite.
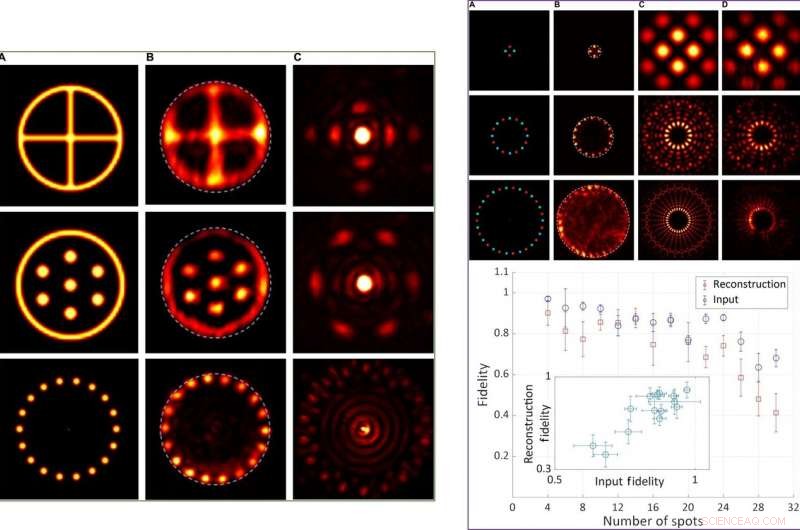
SINISTRA:Risultati sperimentali per oggetti centrosimmetrici a valori reali. Colonna (A) Distribuzioni di intensità degli oggetti reali. Colonna (B) Distribuzione dell'intensità rilevata degli oggetti ricostruiti, utilizzando un'apertura circolare come supporto compatto. Colonna (C) Distribuzioni di intensità di Fourier allo SLM. A DESTRA:Risultati sperimentali e quantitativi per la fedeltà in funzione della complessità dell'oggetto. In alto:distribuzioni di intensità rappresentative di oggetti con 4, 16, e 30 posti. Colonna (A) Distribuzioni di intensità (luminosità) e fase (tonalità) degli oggetti reali. Colonna (B) Distribuzione dell'intensità rilevata degli oggetti ricostruiti, utilizzando un'apertura circolare come supporto compatto. Colonna (C) Distribuzioni di intensità di Fourier calcolate applicate per controllare l'SLM. Colonna (D) Rilevate le corrispondenti distribuzioni di intensità di Fourier dopo le modifiche delle proprietà SLM. In basso:valori di fedeltà quantitativi delle distribuzioni di intensità di Fourier (blu) e delle distribuzioni di intensità dell'oggetto ricostruito (rosso) in funzione del numero di punti nell'oggetto (da 4 a 30). Riquadro:Valori di fedeltà delle distribuzioni di intensità dell'oggetto ricostruito in funzione dei valori di fedeltà delle distribuzioni di intensità di Fourier per tutte le misurazioni. Credito:progressi scientifici, doi:10.1126/sciadv.aax4530.
Nella configurazione sperimentale, Tradonsky et al hanno incluso un laser a cavità degenerata ad anello con un mezzo di guadagno intrinseco, due telescopi 4f e un modulatore di luce spaziale (SLM). Il sistema comprendeva anche un'apertura intracavitaria, Specchi di riflettività 3-D e un accoppiatore di uscita. Il team ha utilizzato i telescopi 4f di sinistra per visualizzare il centro del mezzo di guadagno sull'SLM e ha controllato la trasmissione a ciascun pixel, indipendentemente. Hanno combinato l'apertura intracavità con l'SLM per controllare e formare la distribuzione dell'intensità del laser in uscita. Quando gli scienziati hanno posizionato un'apertura intracavità (maschera di supporto compatta) sul piano di Fourier tra le due lenti, ogni distribuzione di fase ha dimostrato un diverso livello di perdita. Di conseguenza, la distribuzione di fase con perdita minima era la modalità laser più probabile nello studio. Il team ha preso in considerazione due cifre di merito per quantificare la qualità del sistema, inclusa la fedeltà della soluzione e il tempo di calcolo. Il team di ricerca ha ottenuto risultati rappresentativi per oggetti centrosimmetrici con un ottimo accordo tra le distribuzioni di intensità delle forme originali (oggetto reale) e ricostruite.
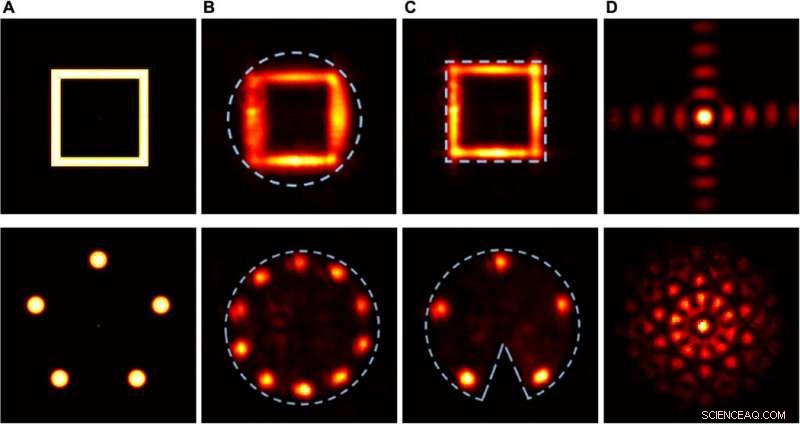
Risultati sperimentali che dimostrano l'effetto qualitativo della tenuta e dell'asimmetria di supporti compatti. Colonna (A) Distribuzione dell'intensità degli oggetti reali. Colonna (B) Distribuzione dell'intensità rilevata degli oggetti ricostruiti, utilizzando un'apertura circolare come supporto compatto. Colonna (C) Distribuzione dell'intensità rilevata degli oggetti ricostruiti, utilizzando un'apertura quadrata come supporto compatto stretto (fila superiore) e un'apertura circolare con un cuneo come supporto compatto asimmetrico (fila inferiore). Colonna (D) Distribuzioni di intensità di Fourier allo SLM. Credito:progressi scientifici, doi:10.1126/sciadv.aax4530
Tradonsky et al hanno misurato l'effetto della complessità degli oggetti sulla fedeltà della ricostruzione e hanno formato distribuzioni di intensità rappresentative per gli oggetti con quattro, 16, e 30 posti. I risultati hanno mostrato che gli oggetti di maggiore complessità (quelli con più punti) hanno mostrato una distribuzione dell'intensità di Fourier di maggiore complessità, con dettagli intricati che non potrebbero essere risolti utilizzando il sistema attuale. Hanno anche notato che le fedeltà di input e ricostruzione diminuiscono con l'aumentare della complessità dell'oggetto, che hanno attribuito al rumore tecnico fluttuante della pompa laser. Hanno condotto esperimenti qualitativi per valutare l'effetto della tenuta e della simmetria durante la ricostruzione dell'oggetto. I risultati hanno mostrato che un supporto compatto e stretto ha migliorato significativamente la qualità dell'oggetto ricostruito.
Il team ha quindi studiato gli effetti quantitativi del raggio dell'apertura del supporto compatto sulla qualità e la fedeltà della ricostruzione. Per oggetti più grandi l'intensità rappresentativa ha subito un rapido decadimento durante la fedeltà della ricostruzione poiché il laser non era in grado di supportare la forma dell'oggetto. Con oggetti più piccoli dell'apertura del supporto compatto, Tradonsky et al hanno osservato un decadimento più lento della fedeltà. In totale, hanno osservato una fedeltà di ricostruzione ridotta quando la fotocamera ha fatto la media su più realizzazioni di un oggetto all'interno del sistema.
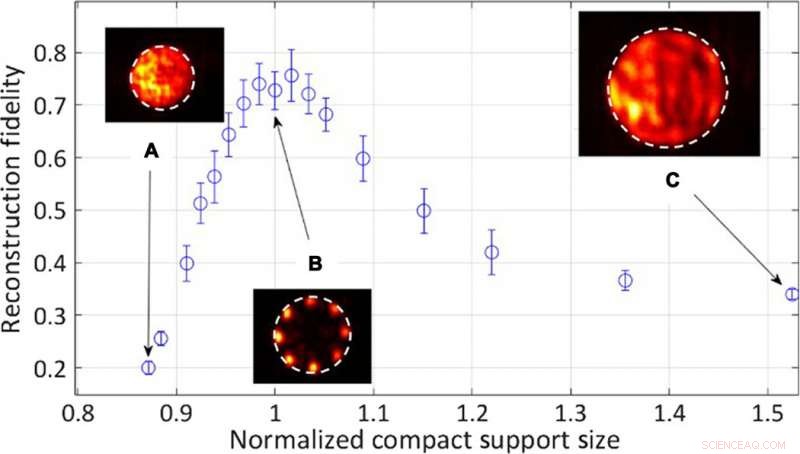
Risultati quantitativi sperimentali per la fedeltà di ricostruzione in funzione del raggio di appoggio compatto dell'apertura normalizzato dalla dimensione dell'oggetto. Riquadri:distribuzioni tipiche dell'intensità degli oggetti ricostruiti. (A) Il raggio di supporto compatto è l'87% del raggio dell'oggetto. (B) Il raggio dell'oggetto è uguale al raggio del supporto compatto. (C) Il raggio di supporto compatto è il 152% del raggio dell'oggetto. Credito:progressi scientifici, doi:10.1126/sciadv.aax4530.
In genere, la risoluzione degli oggetti ricostruiti era relativamente bassa a causa delle aberrazioni di fase nella cavità laser. Il team ha proposto di ottimizzare il sistema e ridurre le aberrazioni per una migliore risoluzione. Gli scienziati hanno anche analizzato il tempo impiegato per offrire una soluzione di ricostruzione utilizzando il sistema e hanno riscontrato che le durate dettate dallo SLM (modulatore di luce spaziale) e dalla lettura della telecamera sono di circa 20 ms. Il tempo di calcolo effettivo del laser è durato solo meno di 100 nanosecondi. Quando Tradonsky et al hanno ottimizzato la configurazione sperimentale utilizzando una disposizione laser a cavità degenerata lineare Q-switched con cellule pockel, hanno ridotto il tempo di calcolo totale del sistema a circa 100 nanosecondi. Comparativamente, il tempo di ricostruzione con l'algoritmo RAAR è durato un secondo.
In questo modo. C. Tradonsky e colleghi hanno presentato un sistema ottico per il recupero rapido della fase utilizzando un nuovo DDCL (laser a cavità degenerata digitale). Il tempo di calcolo è stato di 100 nanosecondi; ordini di grandezza più veloci del convenzionale, sistemi di calcolo basati su algoritmi. In base ai risultati, diverse modifiche al sistema DDCL possono potenzialmente migliorarne le prestazioni, inclusa una maggiore lunghezza della cavità laser per aumentare il numero di indagini parallele indipendenti. Il team di ricerca esplorerà ulteriormente il sistema per risolvere una serie di problemi e risolvere la qualità delle immagini dopo la propagazione attraverso mezzi di diffusione.
© 2019 Scienza X Rete