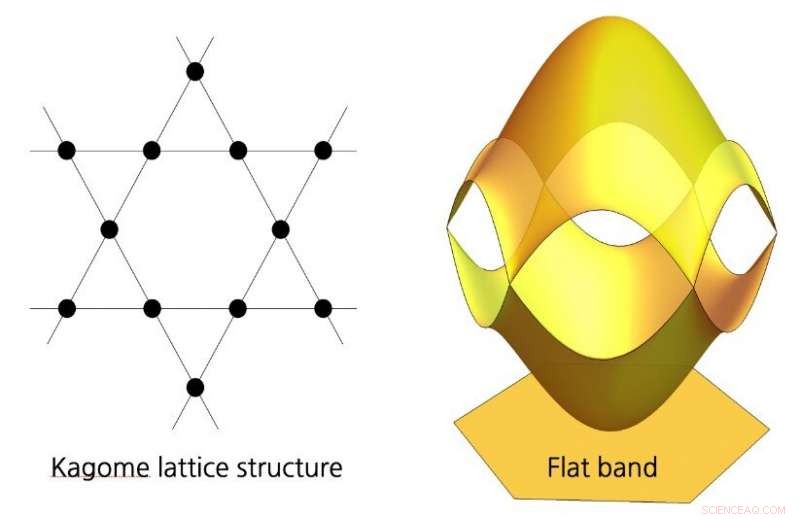
(Sinistra) La struttura reticolare kagome nello spazio reale. (Destra) La struttura a bande corrispondente nello spazio del momento. La banda inferiore è la banda piatta che mostra uno spettro di livello di Landau anomalo. Credito:IBS
La geometria di un oggetto indica la sua forma o il rapporto tra le sue parti. Sapevi che anche gli elettroni nei solidi hanno strutture geometriche? Nella meccanica quantistica, un elettrone nei solidi assume la forma di un'onda con periodicità in modo che lo stato elettronico periodico, il cosiddetto stato di Bloch, può essere caratterizzato specificando la sua energia e momento del cristallo che è proporzionale al suo numero d'onda. La relazione tra l'energia e il momento cristallino degli elettroni è chiamata struttura a bande dei solidi. Per gli elettroni nei solidi, la curvatura di Berry e la metrica quantistica degli stati di Bloch assumono il ruolo della curvatura e della distanza di un oggetto in geometria.
Infatti, la geometria degli stati quantistici è uno dei concetti centrali alla base dei diversi fenomeni fisici, che vanno dal celebre effetto Aharonov-Bohm alle fasi topologiche della materia sviluppate più recentemente. Ad esempio, la curvatura locale di Berry è responsabile del trasporto anomalo di Hall mentre il suo integrale su una varietà chiusa bidimensionale dà il numero di Chern, un numero intero che descrive la conduttività di Hall quantizzata. Però, rispetto alla fisica della curvatura di Berry, gli effetti della metrica quantistica sui fenomeni fisici sono meno compresi, soprattutto nei solidi, sebbene ci siano diversi lavori recenti che propongono gli osservabili fisici relativi alla metrica quantistica. Specialmente, non ci sono state linee guida chiare per la ricerca di materiali in cui si possano osservare le proprietà fisiche relative alla metrica quantistica.
Prof. Yang Bohm-Jung e Dr. Rhim Jun-Won presso il Centro per i sistemi di elettroni correlati all'interno dell'Istituto per le scienze di base (IBS) della Seoul National University, Seul, Corea del Sud, e il Dr. Kim Kyoo presso il Korea Atomic Energy Research Institute, Daejeon, Corea del Sud, hanno riferito di aver trovato un modo per misurare la distanza quantistica degli stati di Bloch nei solidi applicando un campo magnetico. Più specificamente, i ricercatori hanno esaminato lo spettro energetico sotto campo magnetico, chiamato spettro di livello di Landau, di bande piatte nei reticoli kagome e a scacchiera, e osservato un'anomala diffusione del livello di Landau derivante dalla banda piatta. Sorprendentemente, hanno scoperto che la diffusione totale dell'energia del livello di Landau della banda piatta è determinata esclusivamente dalla distanza quantistica massima tra gli stati di Bloch della banda piatta. Vale a dire, la distanza quantistica degli stati di Bloch nel solido può essere misurata applicando un campo magnetico a materiali bidimensionali con bande piatte.
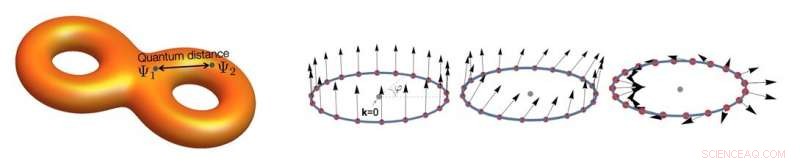
(Sinistra) Un cartone che rappresenta la struttura geometrica degli stati Bloch. La distanza quantistica misura la distanza meccanica quantistica tra due funzioni d'onda di Bloch. (Destra) Le funzioni d'onda di Bloch della banda piatta possono essere rappresentate dallo pseudo-spin (frecce). L'angolo relativo tra due pseudo-spin corrisponde alla distanza quantistica tra i relativi stati di Bloch. Credito:IBS
Recentemente, i materiali bidimensionali con bande piatte hanno ricevuto una grande attenzione come nuova piattaforma per realizzare intriganti stati elettronici. Una banda piatta indica una struttura elettronica a bande in cui l'energia non cambia al variare del momento cristallino. Tali intriganti strutture a banda piatta appaiono in vari reticoli bidimensionali tra cui il reticolo kagome, reticolo della scacchiera, ecc. Il gruppo teorico del team di ricerca IBS CCES si è reso conto che, in molti dei sistemi a banda piatta, la curvatura di Berry degli stati di Bloch è nulla a causa della simmetria del reticolo. Se la curvatura di Berry è strettamente zero, ci si può naturalmente aspettare che la geometria degli stati di Bloch sia determinata unicamente dalla metrica quantistica. Questo aspetto interessante ha motivato il team di teoria dell'IBS a considerare seriamente i materiali bidimensionali con bande piatte come un promettente terreno di gioco per studiare le proprietà fisiche relative alla metrica quantistica.
Infatti, la regola di quantizzazione semiclassica prevede che una normale banda parabolica sotto un campo magnetico formi livelli discreti di Landau equidistanti, e la differenza di energia tra i livelli di Landau vicini è inversamente proporzionale alla massa effettiva degli elettroni. Quando applicato a una banda piatta con una massa efficace infinita, la teoria semiclassica prevede una spaziatura del livello di Landau zero in modo che una banda piatta rimanga inerte sotto il campo magnetico. In questo studio, i ricercatori hanno osservato una natura del tutto peculiare dello spettro di livello di Landau che è in netto contrasto con la norma convenzionale. Hanno riferito che i livelli di Landau delle bande piatte si diffondono nella regione vuota dello spazio energetico dove non sono disponibili stati elettronici in assenza di campo magnetico.
I ricercatori hanno scoperto che la chiave per uno spettro di livello di Landau così insolito è il fatto che la banda piatta nei reticoli kagome e a scacchiera si incrocia con un'altra banda parabolica in un punto. La singolarità nella funzione d'onda della banda piatta derivante dal punto di attraversamento della banda induce un effetto geometrico non banale relativo alla distanza quantistica della funzione d'onda, che a sua volta induce uno spettro di livello di Landau anomalo. Il primo autore, Il dottor Rhim Jun-Won afferma, "Comprendere il ruolo dell'incrocio di banda nelle bande piatte è stata la chiave per descrivere i livelli anomali di Landau. Questa scoperta fornisce un modo pratico per estrarre in modo univoco la distanza quantistica nei solidi".
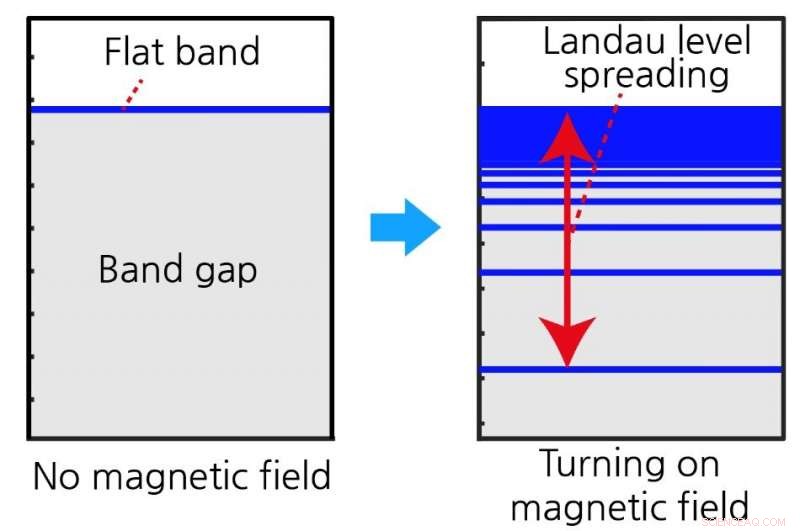
(Sinistra) Lo spettro energetico della banda piatta quando il campo magnetico è assente. Non c'è stato energetico disponibile all'interno del band gap. (Destra) Lo spettro energetico sotto il campo magnetico (i livelli di Landau) derivante dalla banda piatta. I livelli di Landau sono distribuiti nella regione con gap e l'ampiezza della diffusione del livello di Landau è determinata dalla distanza quantistica degli stati di Bloch della banda piatta. Credito:IBS
Questo studio mostra che la distanza quantistica o la metrica quantistica può anche svolgere un ruolo cruciale nel determinare le proprietà dei materiali come fa la curvatura di Berry. Contrariamente ai lavori precedenti, questo studio ha chiaramente identificato i sistemi reticolari candidati in cui l'effetto metrico quantistico è massimizzato mentre l'effetto di curvatura di Berry è ridotto al minimo, e ha scoperto per la prima volta un modo per estrarre direttamente la distanza quantistica nei solidi. Considerando l'enorme impatto del concetto di curvatura di Berry sulla comprensione delle proprietà dei solidi, è naturale aspettarsi che questo studio possa facilitare lo studio futuro sulle proprietà geometriche dei solidi legate alla metrica quantistica e la ricerca di materiali in cui si possano osservare le relative risposte fisiche.
Il prof. Yang Bohm-Jung spiega che "Questo risultato fornirebbe un passo fondamentale verso la comprensione completa delle proprietà geometriche degli stati quantistici nei solidi. Poiché ci sono molte strutture reticolari bidimensionali che ospitano bande piatte, il nostro studio potrebbe innescare future attività di ricerca per scoprire nuovi fenomeni geometrici legati alla metrica quantistica in vari materiali di materia condensata".