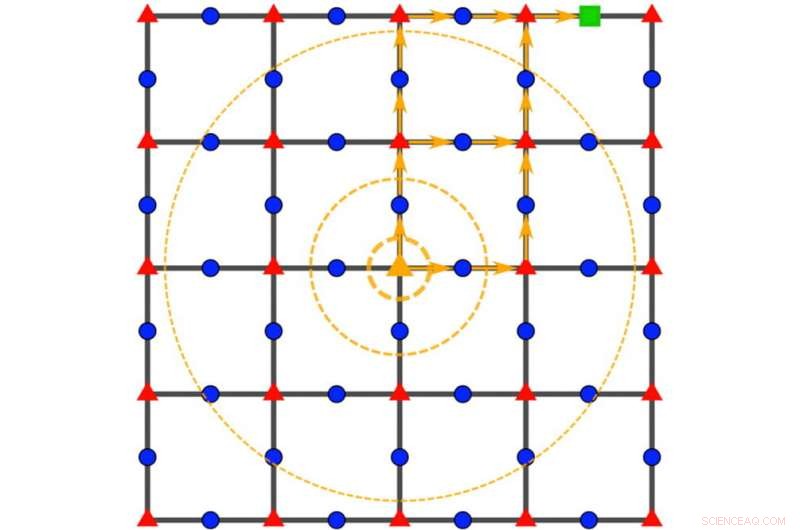
Un grafico della commutatività di Wang-Hazzard cattura i dettagli microscopici delle funzioni matematiche che i fisici usano tipicamente per descrivere l'energia nei sistemi quantistici, riducendo il calcolo dei limiti di velocità quantistica a un'equazione con solo due input. Credito:Zhiyuan Wang/Rice University
I limiti di velocità della natura non sono affissi sui segnali stradali, ma i fisici della Rice University hanno scoperto un nuovo modo per dedurli che è migliore, infinitamente migliore, in alcuni casi, rispetto ai metodi precedenti.
"La grande domanda è, 'Quanto velocemente può qualcosa—informazioni, messa, energia, muoversi nella natura?'", ha detto Kaden Hazzard, un fisico quantistico teorico alla Rice. "Si scopre che se qualcuno ti consegna un materiale, è incredibilmente difficile, generalmente, per rispondere alla domanda».
In uno studio pubblicato oggi sulla rivista dell'American Physical Society PRX Quantum , Lo studente laureato Hazzard e Rice Zhiyuan Wang descrive un nuovo metodo per calcolare il limite superiore dei limiti di velocità nella materia quantistica.
"A livello fondamentale, questi limiti sono molto migliori di quelli disponibili in precedenza, " disse Hazzard, un assistente professore di fisica e astronomia e membro del Rice Center for Quantum Materials. "Questo metodo produce spesso limiti 10 volte più accurati, e non è insolito che siano 100 volte più accurati. In alcuni casi, il miglioramento è così drammatico che troviamo limiti di velocità finiti dove i precedenti approcci prevedevano infiniti".
L'ultimo limite di velocità della natura è la velocità della luce, ma in quasi tutta la materia intorno a noi, la velocità dell'energia e dell'informazione è molto più lenta. frequentemente, è impossibile descrivere questa velocità senza tenere conto del grande ruolo degli effetti quantistici.
Negli anni '70, i fisici hanno dimostrato che le informazioni devono muoversi molto più lentamente della velocità della luce nei materiali quantistici, e sebbene non potessero calcolare una soluzione esatta per le velocità, i fisici Elliott Lieb e Derek Robinson hanno aperto la strada a metodi matematici per calcolare i limiti superiori di tali velocità.
"L'idea è che anche se non posso dirti la velocità massima esatta, posso dirti che la velocità massima deve essere inferiore ad un determinato valore, " Hazzard ha detto. "Se posso dare una garanzia al 100% che il valore reale è inferiore a quel limite superiore, che può essere estremamente utile."
Hazzard ha affermato che i fisici sanno da tempo che alcuni dei limiti prodotti dal metodo Lieb-Robinson sono "ridicolamente imprecisi".
"Si potrebbe dire che le informazioni devono muoversi a meno di 100 miglia all'ora in un materiale quando la velocità reale è stata misurata a 0,01 miglia all'ora, " ha detto. "Non è sbagliato, ma non è molto utile."
I limiti più accurati descritti nel documento PRX Quantum sono stati calcolati con un metodo creato da Wang.
"Abbiamo inventato un nuovo strumento grafico che ci consente di spiegare le interazioni microscopiche nel materiale invece di fare affidamento solo su proprietà più rozze come la sua struttura reticolare, "Ha detto Wang.
Hazzard ha detto Wang, uno studente del terzo anno, ha un incredibile talento nel sintetizzare le relazioni matematiche e nel riformularle in termini nuovi.
"Quando controllo i suoi calcoli, posso andare passo dopo passo, sfornare i calcoli e vedere che sono validi, " Hazzard ha detto. "Ma per capire effettivamente come andare dal punto A al punto B, quale serie di passaggi eseguire quando c'è un'infinita varietà di cose che potresti provare ad ogni passaggio, la creatività è semplicemente incredibile per me."
Il metodo Wang-Hazzard può essere applicato a qualsiasi materiale costituito da particelle che si muovono in un reticolo discreto. Ciò include materiali quantistici spesso studiati come i superconduttori ad alta temperatura, materiali topologici, fermioni pesanti e altri. In ognuno di questi, il comportamento dei materiali nasce da interazioni di miliardi su miliardi di particelle, la cui complessità è al di là del calcolo diretto.
Hazzard ha detto che si aspetta che il nuovo metodo venga utilizzato in diversi modi.
"Oltre alla natura fondamentale di questo, potrebbe essere utile per comprendere le prestazioni dei computer quantistici, in particolare nel capire quanto tempo impiegano a risolvere importanti problemi nei materiali e nella chimica, " Egli ha detto.
Hazzard ha affermato di essere certo che il metodo verrà utilizzato anche per sviluppare algoritmi numerici perché Wang ha dimostrato di poter porre limiti rigorosi agli errori prodotti da tecniche numeriche spesso utilizzate che approssimano il comportamento di grandi sistemi.
Una tecnica popolare che i fisici hanno usato per più di 60 anni consiste nell'approssimare un sistema grande con uno piccolo che può essere simulato da un computer.
"Disegniamo una piccola scatola attorno a un pezzo finito, simulalo e spera che sia abbastanza per approssimare il gigantesco sistema, " Hazzard ha detto. "Ma non c'è stato un modo rigoroso di delimitare gli errori in queste approssimazioni."
Il metodo di calcolo dei limiti di Wang-Hazzard potrebbe portare proprio a questo.
"Esiste una relazione intrinseca tra l'errore di un algoritmo numerico e la velocità di propagazione dell'informazione, "Wang ha spiegato, usando il suono della sua voce e le pareti della sua stanza per illustrare il collegamento.
"Il pezzo finito ha bordi, proprio come la mia stanza ha le pareti. Quando parlo, il suono verrà riflesso dal muro e tornerà a me. In un sistema infinito, non c'è margine, quindi non c'è eco."
Negli algoritmi numerici, gli errori sono l'equivalente matematico degli echi. Risuonano dai bordi della scatola finita, e la riflessione mina la capacità degli algoritmi di simulare il caso infinito. Le informazioni più veloci si muovono attraverso il sistema finito, più breve è il tempo in cui l'algoritmo rappresenta fedelmente l'infinito.
Hazzard ha detto che Wang e altri nel suo gruppo di ricerca stanno usando il loro metodo per creare algoritmi numerici con barre di errore garantite.
"Non dobbiamo nemmeno cambiare gli algoritmi esistenti per metterli in modo rigoroso, barre di errore garantite sui calcoli, " ha detto. "Ma puoi anche capovolgerlo e usarlo per creare algoritmi numerici migliori. Lo stiamo esplorando, e anche altre persone sono interessate a usarli."