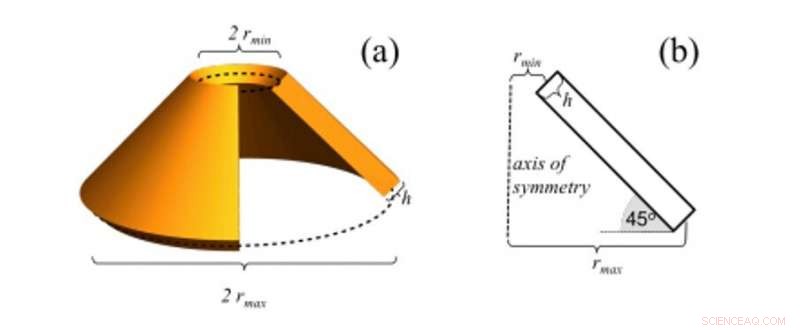
Uno schizzo del cono viscoelastico, e le sue dimensioni. (a) Una vista angolata con una sezione del guscio conico ritagliata. (b) Un diagramma in sezione trasversale comprendente l'asse di simmetria e una singola sezione del guscio conico. Credito:progressi scientifici, doi:10.1126/sciadv.abb2948
Attualmente è difficile determinare la stabilità delle strutture viscoelastiche poiché conformazioni apparentemente stabili possono gradualmente insinuarsi (deformazione plastica di un materiale sotto stress in funzione del tempo) fino a quando la loro stabilità non viene persa. Sebbene un effetto strisciante percepibile non presti necessariamente all'instabilità dei solidi viscoelastici, i ricercatori sono attualmente limitati con simulazioni numeriche per prevedere la stabilità futura rispetto agli strumenti predittivi teorici. In un nuovo rapporto su Progressi scientifici , Erez Y. Urbach e Efi Efrati in fisica e sistemi complessi al Weizmann Institute of Science, Israele, descritto i solidi viscoelastici attraverso una metrica di riferimento istantanea in evoluzione per misurare le deformazioni elastiche. I metodi trasparenti e intuitivi derivati da questo lavoro per i solidi viscoelastici incomprimibili hanno ridotto la questione della stabilità futura ai soli calcoli statici. Il team ha mostrato il potere predittivo dell'approccio comprendendo i sottili meccanismi dell'instabilità ritardata nei sottili gusci elastomerici al fine di dimostrare un accordo quantitativo con gli esperimenti.
Movimento strisciante in natura
Un movimento strisciante relativamente lento è alla base della trappola per mosche di Venere che scatta, uno dei movimenti più veloci nel regno vegetale. Un simile scorrimento si osserva prima che i sottili gusci elastomerici si spezzino, noti come popper saltanti che durano una frazione di secondo. Mentre il lento movimento strisciante delle conchiglie sembra essere elasticamente stabile, durare ordini di grandezza più a lungo, quelli su scala molto più ampia possono essere notati sulla crosta terrestre prima di una scossa di assestamento sismica. I ricercatori stanno ancora imparando il ruolo esatto della viscoelasticità nelle scosse di assestamento a causa dell'assenza di un quadro teorico predittivo per rilevare la futura stabilità di tali sistemi. In ciascuno degli esempi descritti, il lento flusso viscoelastico nel materiale può portare il sistema ad instabilità, provocando un brusco rilascio di energia elastica internamente immagazzinata. Sebbene gli scienziati possano determinare le variabili che governano il comportamento viscoelastico, i meccanismi delle instabilità ritardate nei fluidi viscoelastici rimangono poco conosciuti. In questo lavoro, Urbach ed Efrati hanno affrontato quantitativamente la caratteristica dell'instabilità viscoelastica utilizzando una descrizione metrica.
Rappresentazione schematica della collinearità delle metriche. La minimizzazione della metrica g (contrassegnata da un cerchio nero pieno) è vincolata ed eseguita rispetto al sottoinsieme di metriche che corrispondono a configurazioni realizzabili (linea nera spessa). Queste metriche sono in, particolare, preservare l'orientamento ed euclideo. Data una metrica di riferimento istantaneo, g¯ (contrassegnato da un cerchio grigio pieno), la metrica realizzata corrisponderà al punto dell'insieme delle metriche ammissibili più vicino a g¯ secondo la funzione distanza data dall'energia elastica istantanea. Partendo dal riposo, g¯ evolve da g¯0 (contrassegnato da un cerchio rosso pieno) verso g, che rimane la metrica ammissibile più vicina a g¯ per la collinearità delle tre metriche. Poiché g rimane stazionario, l'evoluzione di g¯ conserverà la collinearità, si avvicina asintoticamente a g¯stat (contrassegnato da un cerchio aperto), che è anche collineare. Sottolineiamo che durante questa evoluzione, g rimane invariato; così, non si osserverà alcuna variazione della configurazione nonostante il rilassamento dello stress. Credito:progressi scientifici, doi:10.1126/sciadv.abb2948 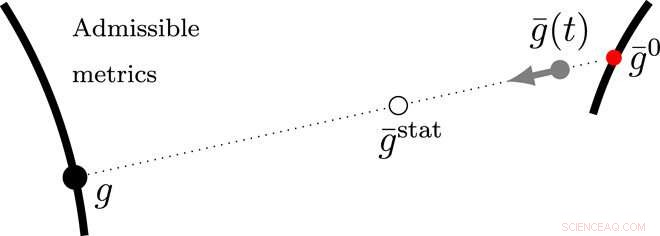
Il team ha descritto il comportamento dei materiali come una risposta elastica rapida rispetto a lunghezze di prova in evoluzione temporale che possono cambiare a causa del lento flusso viscoelastico. Hanno interpretato la risposta microscopica nel materiale e previsto la futura stabilità delle strutture viscoelastiche non vincolate. Urbach et al. spiegato tutte le relazioni dei materiali viscoelastici lineari attraverso intricati calcoli della velocità di deformazione con una funzione di rilassamento dello stress, quindi relazioni matematiche derivate per i sistemi unidimensionali in questo lavoro; alcuni dei quali dipendevano da proprietà del materiale come il modulo di Young e il coefficiente di Poisson. Le deformazioni incrementali istantanee hanno causato un aumento dello stress lineare per una risposta puramente elastica nel materiale. Poiché i materiali viscoelastici tendono ad essere dissipativi (termodinamicamente aperti), la definizione di energia libera elastica può essere incompleta. Gli scienziati hanno quindi eliminato l'inerzia dal sistema e approssimato il moto del materiale a un quasi stato che evolve tra stati di equilibrio elastici. Di conseguenza, una data metrica di riferimento istantanea potrebbe produrre più configurazioni elasticamente stabili.
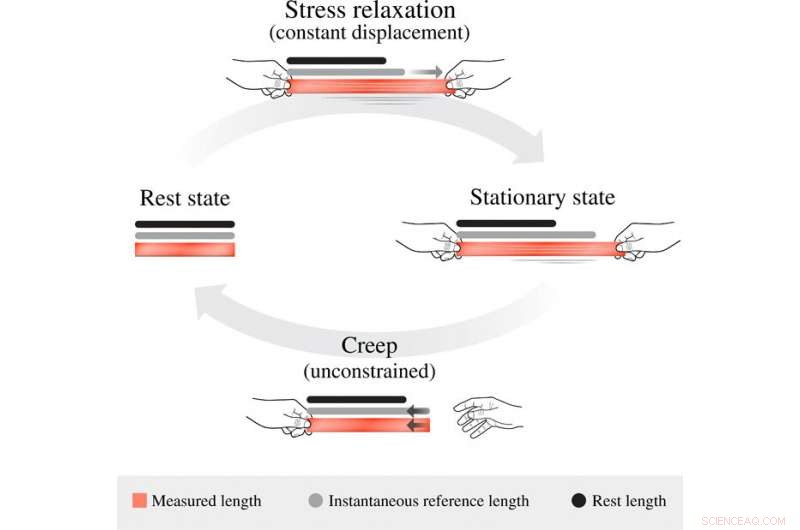
L'evoluzione della lunghezza di riferimento viscoelastica. Allo stato di riposo, tutte e tre le misure di lunghezza sul corpo, la sua lunghezza misurata g (contrassegnata in rosso), la sua lunghezza di riferimento istantanea g¯ (contrassegnata in grigio), e la sua lunghezza di riferimento a riposo g¯0 (contrassegnata in nero) sono tutte uguali. Quando sottoposto a un'estensione di spostamento costante, la lunghezza istantanea di riferimento evolve dalla lunghezza di riposo e verso la lunghezza attualmente assunta, con conseguente rilassamento dello stress. Si avvicina asintoticamente allo stato stazionario g¯stat=βg+(1−β)g¯0, in cui lo stress iniziale è ridotto di un fattore 1 − β. Quando rilasciato, il sistema non vincolato adotta immediatamente la sua lunghezza di riferimento istantanea preferita, quale, a sua volta, si insinua gradualmente verso le lunghezze di riposo. Credito:progressi scientifici, doi:10.1126/sciadv.abb2948
Instabilità viscoelastiche attraverso la descrizione metrica
La metrica di riferimento istantaneo dipendente dal tempo del materiale potrebbe in questo modo evolvere per acquisire nuove configurazioni stabili, unire i punti stabili esistenti, o causare la perdita di stabilità delle configurazioni elastiche stabili. In quest'ultimo scenario, la lenta evoluzione viscoelastica sarà seguita da un rapido scatto, evidenziando la principale difficoltà di prevedere la stabilità delle strutture viscoelastiche. Questa caratteristica è nota come bistabilità temporanea, pseudo bistabilità o deformazione a scorrimento. Affinché i solidi linearmente viscoelastici incomprimibili possano insinuarsi nell'instabilità, devono aver luogo due processi distinti. Primo, uno stato elasticamente stabile acquisirà stabilità attraverso il rilassamento viscoelastico sotto un carico esterno per un certo periodo di tempo. Quindi quando il carico esterno viene rimosso, il corpo assumerà lo stato stabile appena acquisito, insieme al creep viscoelastico per l'instabilità risultante. Però, uno stato stabile acquisito è transitorio (temporaneo). In questo modo, Urbach et al. ha utilizzato la descrizione metrica della viscoelasticità per fornire un quadro del meccanismo che governa la stabilità delle strutture viscoelastiche.
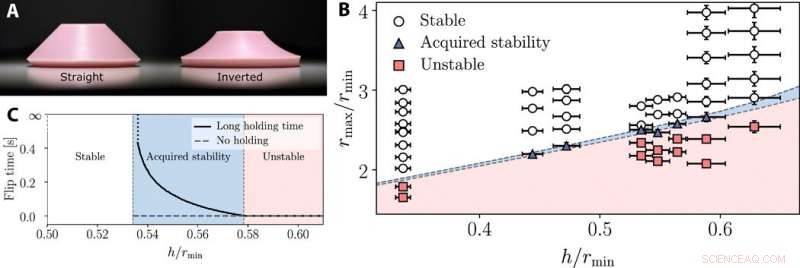
Verifica sperimentale del diagramma di stabilità viscoelastico. (A) Poppers conici diritti e invertiti. Credito fotografico:Erez Y. Urbach, Istituto Weizmann. (B) I due assi abbracciano le proprietà geometriche adimensionali dei popper troncati. I colori di sfondo rappresentano le regioni teoricamente previste di ciascuna delle fasi. Ogni marcatore corrisponde a un popper diverso; marcatori di forma diversa (e colorati) indicano le diverse fasi osservate nell'esperimento. (C) Tempo di rotazione calcolato numericamente in funzione dello spessore normalizzato del popper conico per un rilascio immediato e un lungo tempo di mantenimento. I diversi popper sono stati simulati variando i loro spessori e raggi costanti rmin =10 mm, rmax =25 mm. Le proprietà del materiale prese sono state β =0,1, e si presumeva che il kernel di memoria fosse esponenziale con τ =0,1 s, Modulo di Young E =2,5 MPa, e il rapporto di Poisson v =0,47. La variazione del kernel può portare a un tasso variabile di divergenza del tempo di flipping tra la regione di stabilità stabile e acquisita, tuttavia la posizione di questa divergenza rimarrà invariata. La divergenza dei tempi di flipping è stata affrontata in uno studio precedente, e più recentemente, anche il tasso di divergenza è stato studiato in precedenza. Credito:progressi scientifici, doi:10.1126/sciadv.abb2948
Risultati sperimentali
I calcoli condotti in questo lavoro hanno rivelato molte caratteristiche qualitative delle instabilità viscoelastiche. Gli scienziati hanno quindi testato le previsioni quantitative della teoria esaminando sperimentalmente la risposta dei popper conici in gomma siliconica. Per questo, hanno lanciato bottoni automatici in gomma siliconica come gusci tronco conici per ottenere un controllo più semplice sullo spessore del materiale. All'aumentare dello spessore, la bistabilità è diminuita, poi a un certo punto il popper è scattato immediatamente indietro. Gli scienziati hanno prodotto 50 diversi popper conici di diverse geometrie e hanno testato le loro fasi per determinare sperimentalmente i confini di fase delle proprietà viscoelastiche.
Il lavoro qui presentato era simile a precedenti studi sull'elastoplastica. La teoria metrica può essere implementata su solidi viscoelastici incomprimibili isotropi per fornire regole di base per le instabilità viscoelastiche. Affinché una data struttura possa insinuarsi nell'instabilità, lo strisciamento avrebbe dovuto precedere entro un arco temporale in cui le strutture fossero mantenute sotto un carico esterno. La teoria era particolarmente potente nell'applicazione per descrivere l'instabilità sperimentalmente ritardata nei sottili gusci elastomerici. Questi risultati potranno far luce sul ruolo della viscoelasticità nell'innescare le scosse di assestamento ritardate di un terremoto. In questo modo, la descrizione metrica qui proposta fornirà un quadro teorico per comprendere le instabilità viscoelastiche ritardate.
© 2020 Scienza X Rete