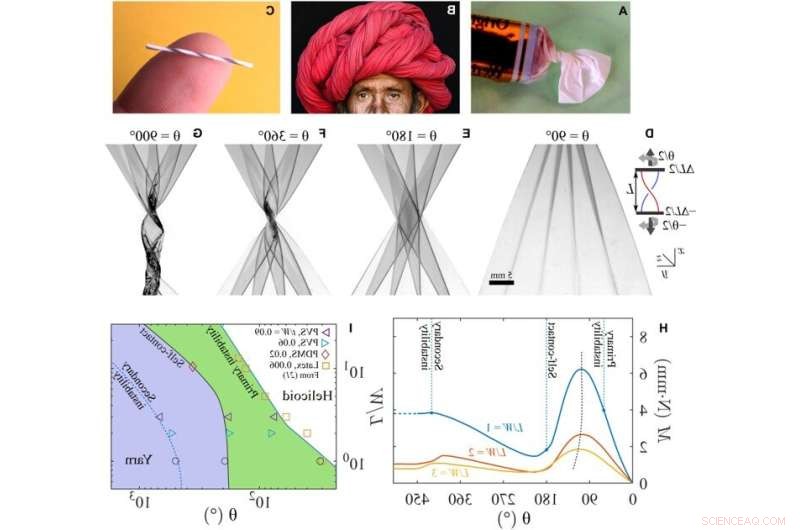
Gli esperimenti rivelano una trasformazione altamente ordinata dei filati quando i fogli tenuti in tensione vengono attorcigliati oltre l'inizio delle instabilità primarie. Esempi di strutture attorcigliate, piegate e a spirale sono i seguenti:(A) caramelle avvolte, (B) turbante Rajashtani multifunzionale (credito fotografico:Lauren Cohen) e (C) filato arrotolato da un foglio di polietilene (vedere la sezione S4). (D a G) Shadowgraph di un foglio PDMS trasparente attorcigliato di un angolo θ come mostrato nel riquadro (L/W =1; t/W =0,0028; ΔL/L =0,1; θp =60 ± 5°). Riquadro:sistema di coordinate schematico e di laboratorio. (D) Rughe osservate appena al di sopra dell'inizio dell'instabilità primaria. (E) Foglio piegato a fisarmonica con autocontatto. (F) Un elicoide annidato con strati piegati che si sviluppano man mano che il foglio viene ulteriormente attorcigliato. (G) L'instabilità dell'instabilità secondaria si verifica con un'ulteriore torsione, risultando in una struttura simile a un filo. La barra della scala è la stessa da (D) a (G). (H) La coppia misurata mostra una variazione ripetuta del dente di sega crescente e decrescente con la torsione. L'ampiezza della variazione aumenta al diminuire di L/W. (I) Una mappa che delinea le regioni in cui l'instabilità primaria, l'auto-contatto e l'instabilità secondaria si verificano in funzione delle proporzioni e della torsione. Le linee sono guide per l'occhio, ad eccezione dell'instabilità primaria per L/W> 3. Credito:Avanzamenti scientifici (2022). DOI:10.1126/sciadv.abi8818
In un nuovo studio ora pubblicato come rapporto e illustrato anche come copertina online di Science Advances , Julien Chopin, Arshad Kudrolli e un team di ricerca in Fisica negli Stati Uniti e in Brasile hanno mostrato come fogli iperelastici ritorti formassero filati multistrato a scorrimento automatico. Incorporando lo stretching dominante con la cinematica pieghevole, hanno misurato la coppia e l'energia derivanti dalle non linearità geometriche. Hanno quindi introdotto un modello geometrico per spiegare la formazione e la struttura di tali filati a scorrimento automatico. I risultati hanno mostrato come una semplice rotazione dell'origami nella struttura tensionale di piegatura a torsione ha portato alla trasformazione di fogli estensibili in architetture autoassemblanti.
Trasformazione della forma dei fogli
Tradizionalmente, i fogli di torsione possono formare filati funzionali che si basano su millenni di pratica umana per formare corde di arco, suture chirurgiche e indossabili in tessuto; tuttavia, la pratica manca ancora di principi generali che guidano la complessità di tali architetture. I filati arrotolati con strutture nidificate possono essere utilizzati per sfruttare l'energia delle batterie e per incorporare materiali amorfi. La piegatura a torsione tensionale può trasformare lastre piatte in strutture a strati tramite la regolazione remota dei confini. La piegatura a torsione e lo scorrimento possono essere utilizzati per riconfigurare e riutilizzare le lenzuola piatte come si vede con il turbante multifunzionale del Rajasthan.
Per comprendere la trasformazione della forma dei fogli e l'interazione tra la topologia e le grandi trasformazioni della forma, Chopin et al hanno utilizzato la scansione a raggi X tridimensionale per dettagliare la formazione spontanea di filati ritorti e multistrato con architetture interne ordinate. Tuttavia, è ancora difficile modellare le grandi trasformazioni e configurazioni di forme. Studi recenti hanno incorporato modelli di piastre elastiche tra cui l'equazione Föppl–von Kármán (FvK) per risolvere la crescita iniziale al di sopra dell'inizio dell'instabilità primaria, ma tali metodi rimangono per spiegare la trasformazione di un foglio piatto in filati a spirale. In questo lavoro, Chopin et al hanno sviluppato una nuova struttura per combinare la cinematica dei fogli strutturati e hanno utilizzato gli origami per spiegare queste osservazioni. Il team ha mostrato come i fogli piegati mostrassero forme poligonali regolari come descritto dai simboli Schläfli e come la cinematica degli origami catturasse le caratteristiche principali della struttura per fornire una struttura che servisse da guida per lo sviluppo di materiali iperelastici con ampie applicazioni.
Copertina in linea:un sottile foglio di polidimetilsilossano (PDMS) è attorcigliato in un filato a spirale multistrato. Per millenni, gli esseri umani hanno attorcigliato fogli elastici per formare filati funzionali per creare capi di abbigliamento, strumenti a corda e plastica riciclata. Chopin e Kudrolli, sviluppano una struttura elasto-geometrica per comprendere i meccanismi fisici coinvolti nella torsione dei fogli estensibili in architetture autoassemblate per strategie di produzione avanzate. Credito:Progressi scientifici (2022). DOI:10.1126/sciadv.abi8818
Il team ha mostrato esempi di fogli di polidimetilsilossano (PDMS) con torsione crescente. Man mano che la torsione applicata aumentava ulteriormente, hanno notato la formazione di una struttura elicoidale annidata in vita, seguita da instabilità secondarie e risultanti piegature ricorsive e un filato multistrato arrotolato. Ogni grande trasformazione di forma faceva sì che la velocità di variazione della coppia applicata cambiasse segno e formasse una variazione a dente di sega con una torsione.
Chopin et al. hanno illustrato la struttura di torsione tensionale per comprendere le principali fasi osservate di trasformazione di un foglio planare in filati a scorrimento automatico. Ci sono riusciti introducendo una serie di modelli per combinare geometria, elasticità e cinematica per poi catturare le trasformazioni di forma osservate. I ricercatori hanno catturato l'energia elastica immagazzinata e la risposta torsionale e hanno seguito questo lavoro con la tomografia a raggi X 3D per ricostruire fogli di polivinilsilossano (PVS) ritorti. Gli scienziati hanno quindi calcolato la densità di energia di flessione utilizzando fogli con vari moduli di Young e caratterizzato il trasferimento con torsione.
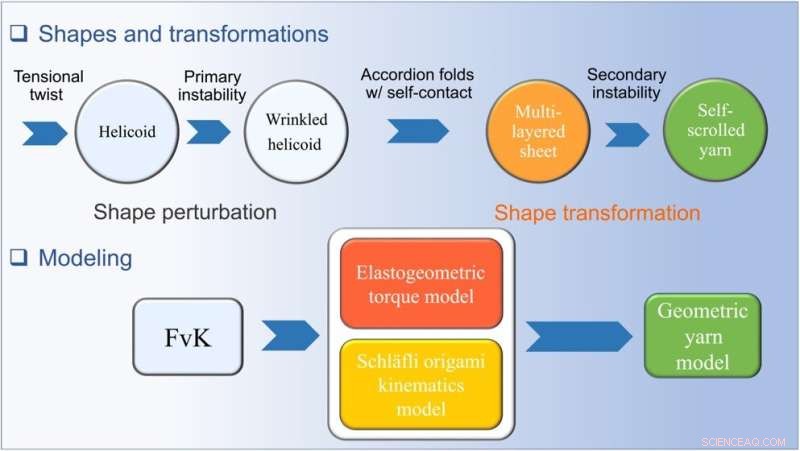
Una panoramica delle trasformazioni di osservazione con la torsione e la struttura torsione-piegatura tensionale. Le principali trasformazioni osservate come un foglio planare sperimentano la piegatura a torsione tensionale e lo scorrimento con la torsione applicata. Viene mostrata la struttura elastogeometrica, incluso il formalismo perturbativo FvK, il modello di coppia elastogeometrica che incorpora non linearità geometriche per spiegare la relazione sforzo-deformazione con la torsione, il modello cinematico origami di Schläfli e il modello di filato geometrico. Credito:Progressi scientifici (2022). DOI:10.1126/sciadv.abi8818
Modello elastogeometrico torque, autopiegante e origami Schläfli
Sulla base delle osservazioni sperimentali, Chopin et al. hanno sviluppato un modello elastogeometrico per calcolare l'energia elastica immagazzinata e la risposta torsionale del foglio. Ci sono riusciti traendo ispirazione dalla teoria del campo tensionale per descrivere lastre altamente rugose, dove le sollecitazioni di flessione e compressione erano trascurabili rispetto alle trecce di trazione. Come nella teoria del campo tensionale, Chopin et al presumevano che l'energia durante il ripiegamento fosse data principalmente dalle modalità di allungamento nella direzione longitudinale, mentre le modalità di flessione erano subdominanti. Il team ha confrontato la coppia misurata in funzione della torsione relativa alla natura iperelastica del materiale e ha integrato la propria analisi elastogeometrica con la costruzione di origami per mostrare un buon accordo tra la forma dell'origami e il foglio attorcigliato. Gli scienziati hanno quindi identificato questi origami utilizzando i simboli Schläfli, che hanno poi chiamato Schläfli origami. Variando i simboli Schläfli, Chopin et al. hanno ottenuto inviluppi a forma di triangolo, pentagono, ettagono e nonagonale. Il lavoro ha evidenziato come la cinematica degli origami fosse alla base della piegatura della torsione tensionale.
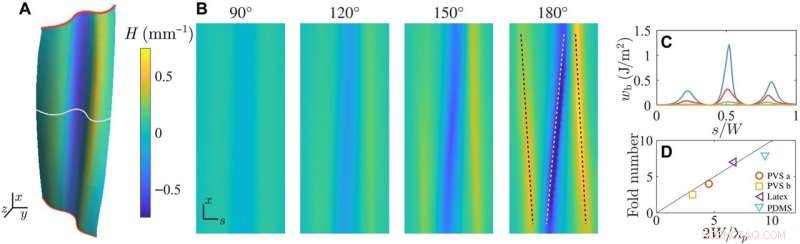
Ripiegamento a fisarmonica tramite localizzazione della curvatura. (A) La deformazione di un foglio di polivinilsilossano (PVS) ritorto di θ =120° ottenuto con tomografia a raggi X e reso con curvatura media H data dalla barra dei colori a destra (L/W =3; t/W =0,009; θp =75°±5°). Viene mostrato l'80% centrale del foglio lontano dai morsetti. (B) La distribuzione spaziale H mappata su un dominio rettangolare mostra la rottura della simmetria e la localizzazione della curvatura del foglio con torsione. (C) Il contenuto di piegatura wb mostra la localizzazione dell'energia con la piega attraverso la sezione trasversale indicata dalla linea bianca continua in (A). (D) Il numero misurato di pieghe n confrontato con la relazione data dalla lunghezza d'onda dell'instabilità primaria n =2W/λp. Le proporzioni (t/W, L/W) sono le seguenti:PVS a (0.009,2), PVS b (0.006,3), PDMS (0.003,1) e lattice (0.003,2). I tre materiali sono iperelastici con modulo di Young E =1,2 MPa (PVS), 6,2 MPa (PDMS) e 3,6 MPa (lattice). Credito:Progressi scientifici (2022). DOI:10.1126/sciadv.abi8818
La formazione del filato e il modello geometrico del filato
Per modellare la crescita del filo, Chopin et al hanno ipotizzato che il foglio potesse essere diviso in tre sezioni, per includere una struttura di lunghezza simile a un filo e due strutture a ventaglio. Questa semplificazione ha consentito loro di mantenere il ruolo fondamentale del bordo della lamiera ritorta nel modello di coppia elastogeometrica. Hanno anche studiato l'evoluzione della lunghezza del filo avvolgendo elicoidalmente i bordi della ventola attorno a un'anima cilindrica di un diametro specifico per formare in definitiva un modello di crescita in buon accordo con i dati sperimentali.
L'origami Schläfli parziale spiega le architetture a strati a mezza torsione. (A) Forme geometriche ottenute aumentando i simboli Schläfli e il numero di sfaccettature. (B) Confronto tra il radiogramma sperimentale e l'origami piega Schläfli. Si osserva una buona corrispondenza in tutti e quattro i casi. (C) L'angolo Ψi della i-esima piega in funzione dell'angolo i α calcolato utilizzando il modello geometrico è in ottimo accordo. (D) Confronto dell'angolo apicale α come funzione calcolata α utilizzando vari fogli e caricamento. (E) L'angolo al vertice in funzione del numero del triangolo è essenzialmente costante. Credito:Progressi scientifici (2022). DOI:10.1126/sciadv.abi8818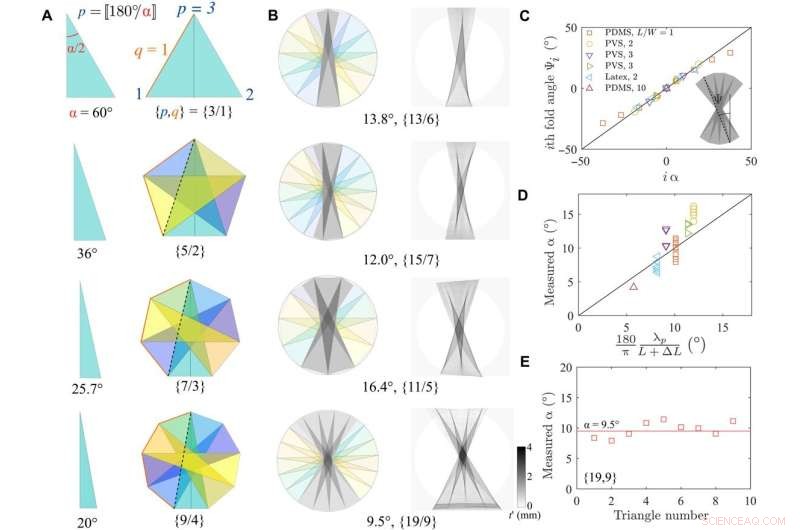
In questo modo Julien Chopin, Arshad Kudrolli e colleghi hanno descritto la trasformazione straordinariamente ordinata di fogli piatti in filati multistrato scrollati. Hanno raggiunto questo obiettivo introducendo una serie di modelli elastogeometrici semplificati per formare una struttura tensionale pieghevole a torsione. Il team ha esplorato la struttura piatta multistrato introducendo un modello di origami Schläfli, in cui gli origami, quando attorcigliati da un mezzo giro, formavano poligoni regolari a forma di stella caratterizzati da simboli Schläfli. Chopin et al hanno utilizzato l'analisi tomografica a raggi X per spiegare l'evoluzione del foglio e hanno indicato la composizione di una regione di filo altamente ritorto al centro e regioni a ventaglio debolmente ritorte collegate ai due morsetti. Il modello incorporato in questo lavoro si basava su una cinematica semplificata per fornire una struttura per consentire filati multifunzionali utilizzando polimeri ultrasottili, nanotubi di carbonio e fogli di grafene, adatti come materiali con applicazioni in medicina ed elettronica flessibile. Gli scienziati hanno utilizzato polimeri PDMS (polidimetilsilossano) e PVS (polivinilsilossano) a causa della loro iperelasticità in diverse condizioni di carico. La strategia di piegatura a torsione risultante può creare strutture funzionali ridistribuibili da elementi semplici per una produzione avanzata con materiali morbidi. + Esplora ulteriormente
© 2022 Rete Science X