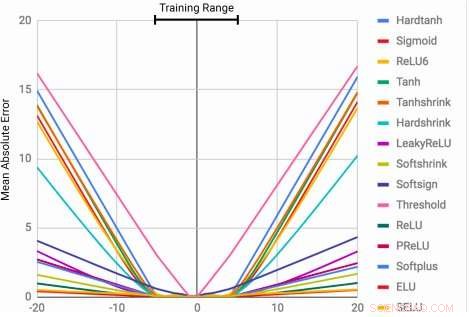
Gli MLP apprendono la funzione di identità solo per i valori di intervallo su cui sono addestrati. L'errore medio aumenta notevolmente sia al di sotto che al di sopra della gamma di numeri osservati durante l'allenamento. Credito:Trask et al.
La capacità di rappresentare e manipolare quantità numeriche può essere osservata in molte specie, compresi gli insetti, mammiferi e umani. Ciò suggerisce che il ragionamento quantitativo di base è una componente importante dell'intelligenza, che ha diversi vantaggi evolutivi.
Questa capacità potrebbe essere molto preziosa nelle macchine, consentendo il completamento più rapido ed efficiente delle attività che comportano la manipolazione dei numeri. Ancora, finora, le reti neurali addestrate a rappresentare e manipolare le informazioni numeriche sono state raramente in grado di generalizzare ben al di fuori della gamma di valori incontrati durante il processo di addestramento.
Un team di ricercatori di Google DeepMind ha recentemente sviluppato una nuova architettura che affronta questa limitazione, ottenere una migliore generalizzazione sia all'interno che all'esterno dell'intervallo di valori numerici su cui è stata addestrata la rete neurale. Il loro studio, che è stato pre-pubblicato su arXiv, potrebbe informare lo sviluppo di strumenti di apprendimento automatico più avanzati per completare le attività di ragionamento quantitativo.
"Quando le architetture neurali standard vengono addestrate a contare fino a un numero, spesso faticano a contare fino a uno più alto, "Andrea Trask, ricercatore capo del progetto, ha detto a Tech Xplore. "Abbiamo esplorato questa limitazione e abbiamo scoperto che si estende anche ad altre funzioni aritmetiche, portando alla nostra ipotesi che le reti neurali apprendano i numeri in modo simile a come apprendono le parole, come un vocabolario finito. Ciò impedisce loro di estrapolare correttamente le funzioni che richiedono numeri (più alti) non visti in precedenza. Il nostro obiettivo era proporre una nuova architettura che potesse eseguire una migliore estrapolazione."

Il Neural Accumulator (NAC) è una trasformazione lineare dei suoi input. La matrice di trasformazione è il prodotto per elemento di tanh (Wˆ ) e σ(Mˆ ). L'unità di logica aritmetica neurale (NALU) utilizza due NAC con pesi legati per consentire l'addizione/sottrazione (cella viola più piccola) e la moltiplicazione/divisione (cella viola più grande), controllato da un cancello (cella arancione). Credito:Trask et al.
I ricercatori hanno ideato un'architettura che incoraggia un'estrapolazione numerica più sistematica rappresentando le quantità numeriche come attivazioni lineari che vengono manipolate utilizzando operatori aritmetici primitivi, che sono controllati da porte apprese. Hanno chiamato questo nuovo modulo unità logica aritmetica neurale (NALU), ispirato all'unità logica aritmetica dei processori tradizionali.
"I numeri sono solitamente codificati nelle reti neurali utilizzando rappresentazioni one-hot o distribuite, e le funzioni sui numeri vengono apprese all'interno di una serie di livelli con attivazioni non lineari, " Ha spiegato Trask. "Proponiamo che i numeri dovrebbero invece essere memorizzati come scalari, memorizzare un singolo numero in ogni neurone. Per esempio, se volessi memorizzare il numero 42, dovresti solo avere un neurone contenente un'attivazione di esattamente '42, ' invece di una serie di neuroni 0-1 che lo codificano."
I ricercatori hanno anche cambiato il modo in cui la rete neurale apprende le funzioni su questi numeri. Invece di utilizzare architetture standard, che può apprendere qualsiasi funzione, hanno ideato un'architettura che propaga in avanti un insieme predefinito di funzioni che sono viste come potenzialmente utili (ad es. moltiplicazione o divisione), utilizzando architetture neurali che apprendono meccanismi di attenzione su queste funzioni.
"Questi meccanismi di attenzione decidono poi quando e dove ogni funzione potenzialmente utile può essere applicata invece di apprendere quella funzione stessa, " Ha detto Trask. "Questo è un principio generale per la creazione di reti neurali profonde con un bias di apprendimento desiderabile sulle funzioni numeriche".

(sopra) Fotogrammi dall'attività di monitoraggio del tempo gridworld. L'agente (grigio) deve spostarsi verso la destinazione (rosso) a un'ora specificata. (sotto) NAC migliora la capacità di estrapolazione appresa dagli agenti A3C per il compito di datazione. Credito:Trask et al.
Il loro test ha rivelato che le reti neurali potenziate da NALU potrebbero imparare a svolgere una varietà di compiti, come il monitoraggio del tempo, eseguire funzioni aritmetiche su immagini di numeri, tradurre il linguaggio numerico in scalari a valori reali, esecuzione di codice informatico e conteggio di oggetti nelle immagini.
Rispetto alle architetture convenzionali, il loro modulo ha raggiunto una generalizzazione significativamente migliore sia all'interno che all'esterno della gamma di valori numerici con cui è stato presentato durante la formazione. Anche se NALU potrebbe non essere la soluzione ideale per ogni compito, il loro studio fornisce una strategia di progettazione generale per la creazione di modelli che funzionano bene su una particolare classe di funzioni.
"L'idea che una rete neurale profonda dovrebbe selezionare da un insieme predefinito di funzioni e apprendere i meccanismi di attenzione che governano dove vengono utilizzate è un'idea molto estensibile, " ha spiegato Trask. "In questo lavoro, abbiamo esplorato semplici funzioni aritmetiche (addizione, sottrazione, moltiplicazione e divisione), ma siamo entusiasti del potenziale per apprendere meccanismi di attenzione su funzioni molto più potenti in futuro, forse portando gli stessi risultati di estrapolazione che abbiamo osservato in un'ampia varietà di campi".
© 2018 Tech Xplore