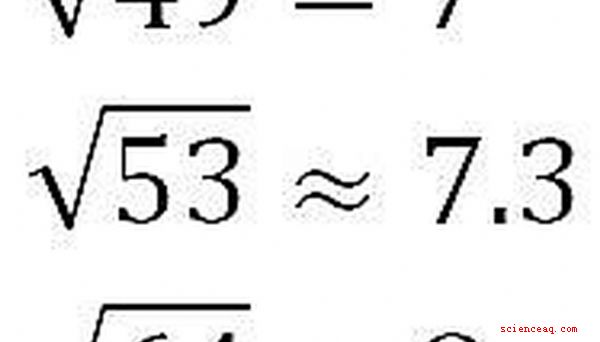
In matematica, a volte è importante per noi essere in grado di stimare i valori delle radici quadrate (radicali). Questo è specialmente il caso degli esami che non consentono l'uso di una calcolatrice e stai cercando di eliminare le risposte sbagliate o di verificare la ragionevolezza della risposta. Inoltre, in geometria, i valori sqrt (2) e sqrt (3) vengono visualizzati così frequentemente che è essenziale conoscere i loro valori approssimativi.

Questo articolo mostra i passaggi per stimare una radice quadrata. L'articolo presuppone che tu abbia una conoscenza di base delle radici quadrate e dei quadrati perfetti. Vedi la sezione di riferimento per ulteriori informazioni.

Per stimare il valore della radice quadrata di un numero, trova i quadrati perfetti sopra e sotto il numero. Per esempio, per stimare sqrt (6), nota che 6 è tra i quadrati perfetti 4 e 9. Sqrt (4) = 2, e sqrt (9) = 3. Poiché 6 è più vicino a 4 che a 9, noi Ci si aspetta che la sua radice quadrata sia più vicina al 2 che al 3. In realtà è circa 2.4, ma finché sapevi che era in quello stadio, staresti bene. Anche solo sapere che era tra 2 e 3 sarebbe vantaggioso.

Proviamo con un altro esempio. Stima sqrt (53). 53 è tra i quadrati perfetti 49 e 64, le cui radici quadrate sono 7 e 8, rispettivamente. 53 è più vicino a 49 che a 64, quindi sarebbe ragionevole stimare che sqrt (53) sia compreso tra 7 e 7,5. Si scopre che si tratta di 7.3.

Ci sono due radici quadrate che emergono molto frequentemente in geometria. Sono sqrt (2) e sqrt (3). È molto importante che memorizzi i loro valori approssimativi. Si noti che sqrt (1) è 1 e sqrt (4) è 2. In base a ciò, non dovrebbe sorprendere che sqrt (2) sia circa 1.4 e sqrt (3) sia circa 1.7.

La cosa più importante è ricordare che sqrt (2) è maggiore di 1, e sqrt (3) è minore di 2. Un altro articolo discute l'applicazione di queste radici quadrate nel lavorare con triangoli rettangoli e il teorema di Pitagora.

Gli studenti dovrebbero assicurarsi di sentirsi a proprio agio nella stima delle radici quadrate e, per questo, stimare tutte le loro risposte per vedere se sono ragionevoli. Questo di solito ti consente di cogliere i tuoi errori prima di consegnare gli esami.