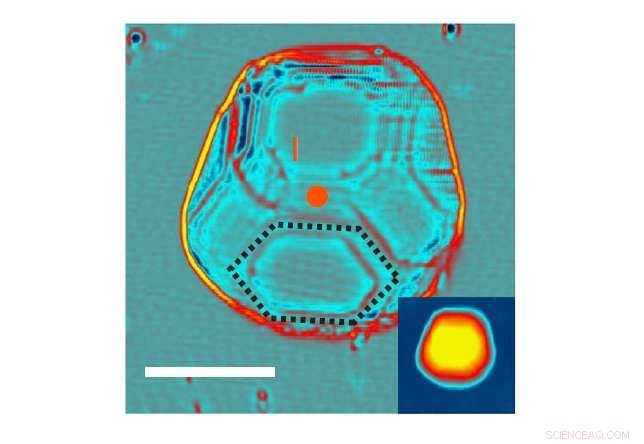
Immagine topografica di un nanocristallo di piombo utilizzato nello studio. Barra della scala:10 nm. Credito:Vlaic et al. Comunicazioni sulla natura
Per la prima volta, i fisici hanno convalidato sperimentalmente una congettura del 1959 che pone dei limiti a quanto piccoli possono essere i superconduttori. La comprensione della superconduttività (o della sua mancanza) su scala nanometrica dovrebbe essere importante per la progettazione di futuri computer quantistici, tra le altre applicazioni.
Nel 1959, il fisico P.W. Anderson ha ipotizzato che la superconduttività possa esistere solo in oggetti abbastanza grandi da soddisfare determinati criteri. Vale a dire, l'energia del gap superconduttore dell'oggetto deve essere maggiore della sua spaziatura del livello di energia elettronica e questa spaziatura aumenta man mano che le dimensioni diminuiscono. Il punto di cutoff (dove i due valori sono uguali) corrisponde ad un volume di circa 100 nm 3 . Fino ad ora non è stato possibile testare sperimentalmente il limite di Anderson a causa delle difficoltà nell'osservare gli effetti dei superconduttori a questa scala.
Nel nuovo studio pubblicato su Comunicazioni sulla natura , Sergio Vlaic e coautori dell'Università Paris Sciences et Lettres e del Centro nazionale francese per la ricerca scientifica (CNRS) hanno progettato un nanosistema che ha permesso loro di studiare sperimentalmente il limite di Anderson per la prima volta.
Il limite di Anderson sorge perché, a scale molto piccole, i meccanismi alla base della superconduttività essenzialmente smettono di funzionare. Generalmente, la superconduttività si verifica quando gli elettroni si legano insieme per formare coppie di Cooper. Le coppie di Cooper hanno un'energia leggermente inferiore rispetto ai singoli elettroni, e questa differenza di energia è l'energia del gap superconduttore. La minore energia delle coppie Cooper inibisce le collisioni di elettroni che normalmente creano resistenza. Se l'energia del gap superconduttore diventa troppo piccola e svanisce, il che può verificarsi, Per esempio, quando la temperatura aumenta, le collisioni di elettroni riprendono e l'oggetto smette di essere un superconduttore.
Il limite di Anderson mostra che le piccole dimensioni sono un altro modo in cui un oggetto può smettere di essere un superconduttore. Però, a differenza degli effetti dell'aumento della temperatura, questo non è perché gli oggetti più piccoli hanno un'energia di gap superconduttore più piccola. Anziché, sorge perché i cristalli più piccoli hanno meno elettroni, e quindi meno livelli di energia degli elettroni, rispetto ai cristalli più grandi. Poiché l'energia totale possibile dell'elettrone di un elemento rimane la stessa, indipendentemente dalle dimensioni, i cristalli più piccoli hanno spazi maggiori tra i loro livelli di energia degli elettroni rispetto ai cristalli più grandi.
Secondo Anderson, questa grande distanza tra i livelli di energia elettronica dovrebbe rappresentare un problema, e si aspettava che la superconduttività scomparisse quando la distanza diventa maggiore dell'energia del gap superconduttore. La ragione di questo, parlando in generale, è che una conseguenza dell'aumento della spaziatura è una diminuzione dell'energia potenziale, che interferisce con la competizione tra energia cinetica e potenziale necessaria perché si verifichi la superconduttività.
Per indagare cosa succede alla superconduttività degli oggetti intorno al limite di Anderson, gli scienziati nel nuovo studio hanno preparato grandi quantità di nanocristalli di piombo isolati che variano in volume da 20 a 800 nm 3 .
Sebbene non potessero misurare direttamente la superconduttività di oggetti così piccoli, i ricercatori potrebbero misurare qualcosa chiamato effetto di parità, che deriva dalla superconduttività. Quando un elettrone viene aggiunto a un superconduttore, l'energia aggiuntiva è in parte influenzata dal fatto che vi sia un numero pari o dispari di elettroni (la parità), che è dovuto agli elettroni che formano coppie di Cooper. Se gli elettroni non formano coppie di Cooper, non vi è alcun effetto di parità, indicando l'assenza di superconduttività.
Sebbene l'effetto di parità sia stato precedentemente osservato in grandi superconduttori, questo studio è la prima volta che è stato osservato in piccoli nanocristalli che si avvicinano al limite di Anderson. In accordo con le previsioni di Anderson di più di 50 anni fa, i ricercatori hanno osservato l'effetto di parità per i nanocristalli più grandi, ma non per i nanocristalli più piccoli al di sotto di circa 100 nm 3 .
I risultati non solo convalidano la congettura di Anderson, ma si estendono anche ad un ambito più generale, i modelli Richardson-Gaudin. Questi modelli sono equivalenti alla teoria convenzionale della superconduttività, la teoria di Bardeen Cooper Schrieffer, per oggetti molto piccoli.
"La nostra dimostrazione sperimentale della congettura di Anderson è anche una dimostrazione della validità dei modelli Richardson-Gaudin, " ha detto il coautore Hervé Aubin dell'Università Paris Sciences et Lettres e del CNRS Phys.org . "I modelli Richardson-Gaudin sono un importante pezzo di lavoro teorico perché possono essere risolti esattamente e possono essere applicati a un'ampia gamma di sistemi; non solo ai nanocristalli superconduttori ma anche ai nuclei atomici e al gas atomico fermionico freddo, dove protoni e neutroni, che sono fermioni come gli elettroni, possono anche formare coppie Cooper."
Dal lato più pratico, i ricercatori si aspettano che i risultati abbiano applicazioni nei futuri computer quantistici.
"Una delle applicazioni più interessanti delle isole superconduttrici è il loro uso come scatole di coppia Cooper impiegate nei bit quantistici, l'unità elementare di un ipotetico computer quantistico, " Aubin ha detto. "Finora, Le coppie di scatole Cooper utilizzate nei qubit sono molto più grandi del limite di Anderson. Riducendo le dimensioni della scatola della coppia Cooper, gli ingegneri informatici quantistici alla fine dovranno far fronte alla superconduttività al limite di Anderson".
© 2017 Phys.org