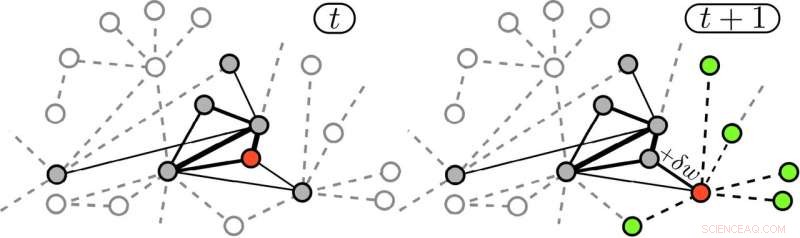
Le passeggiate casuali rinforzate dai bordi producono una coevoluzione della rete con le dinamiche dei camminatori. Al momento t il camminatore è sul nodo rosso e ha già visitato i nodi grigi, mentre i nodi ombreggiati sono ancora inesplorati. Le larghezze dei bordi sono proporzionali ai loro pesi. Al tempo t + 1 il camminatore si è spostato su un nodo vicino (rosso), e il peso del bordo utilizzato è stato rinforzato da δw. A questo punto, il camminatore tornerà preferibilmente indietro, sebbene possa anche accedere all'insieme di 'adiacente possibile' (verde). Credito:Iacopo Iacopini
I ricercatori della Queen Mary University di Londra hanno sviluppato un modello matematico per l'emergere delle innovazioni.
Studiare i processi creativi e comprendere come nascono le innovazioni e come le novità possono innescare ulteriori scoperte potrebbe portare a interventi efficaci per alimentare il successo e la crescita sostenibile della società.
I risultati empirici hanno dimostrato che il modo in cui vengono scoperte le novità segue modelli simili in una varietà di contesti diversi, tra cui scienza, arti, e tecnologia.
Lo studio, pubblicato in Lettere di revisione fisica , introduce un nuovo quadro matematico che riproduce correttamente la velocità con cui emergono le novità nei sistemi reali, nota come legge di Heaps, e può spiegare perché le scoperte sono fortemente correlate e spesso arrivano in gruppi.
Lo fa traducendo la teoria dell'"adiacente possibile", inizialmente formulato da Stuart Kauffman nel contesto dei sistemi biologici, nel linguaggio delle reti complesse. L'adiacente possibile è l'insieme di tutte le nuove opportunità che si aprono quando viene fatta una nuova scoperta. Le reti sono emerse come un potente mezzo per investigare i sistemi del mondo reale, catturando le relazioni essenziali tra i componenti, e modellare la struttura nascosta dietro molti complessi fenomeni sociali.
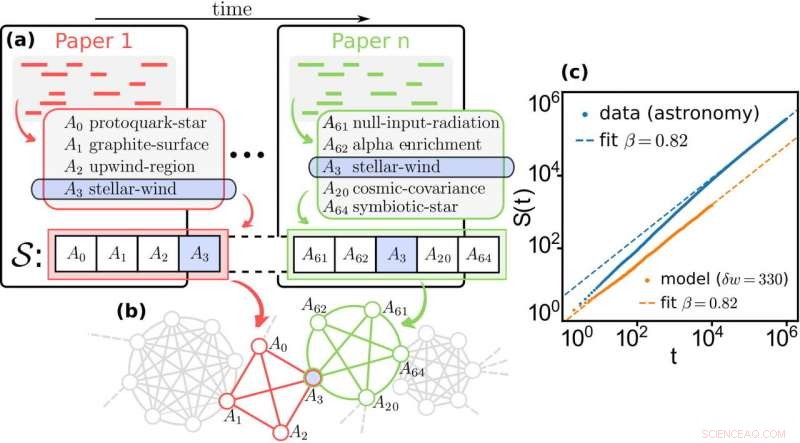
Crescita della conoscenza nella scienza. (a) Una sequenza empirica di concetti scientifici S viene estratta da una sequenza ordinata temporalmente di articoli concatenando, per ogni settore scientifico, i concetti rilevanti presenti negli abstract. (b) La rete di relazioni tra concetti si costruisce collegando tutti i concetti che compaiono nello stesso abstract. La rete viene quindi utilizzata come struttura sottostante per l'esecuzione del nostro modello random walk rinforzato con bordi. (c) Il modello viene quindi sintonizzato sui dati empirici selezionando la quantità di rinforzo δw che riproduce l'esponente di Heaps β ottenuto adattando la curva di Heap estratta da S come legge di potenza. Credito:Iacopo Iacopini
In questo lavoro, le reti sono utilizzate per modellare lo spazio sottostante delle relazioni tra i concetti.
L'autore principale Professor Vito Latora, dalla Queen Mary's School of Mathematics Sciences, ha dichiarato:"Questa ricerca apre nuove direzioni per la modellizzazione dell'innovazione, insieme a un nuovo quadro che potrebbe diventare importante nello studio di tecnologie, biologico, artistico, e sistemi commerciali”.
Ha aggiunto:"Studiare i processi attraverso i quali nascono le innovazioni può aiutare a comprendere gli ingredienti principali dietro un'idea vincente, una tecnologia innovativa o un'attività commerciale di successo, ed è fondamentale per elaborare decisioni efficaci informate sui dati, strategie, e interventi per alimentare il successo e la crescita sostenibile della nostra società".
Nello studio, il processo di scoperta è modellato come una particolare classe di passeggiate casuali, chiamate passeggiate "rinforzate", su una sottostante rete di relazioni tra concetti e idee. Un'innovazione corrisponde alla prima visita di un sito della rete, e ogni volta che un camminatore passa da un concetto all'altro, tale associazione (un margine della rete) viene rafforzata in modo da essere utilizzata più frequentemente in futuro. I ricercatori hanno chiamato questo modello "camminata casuale rinforzata dal bordo".
Per mostrare come funziona il modello in un caso reale, hanno anche costruito un dataset di 20 anni di pubblicazioni scientifiche in diverse discipline, come l'astronomia, ecologia, economia e matematica per analizzare la comparsa di nuovi concetti. Ciò ha dimostrato che, nonostante la sua semplicità, il modello random walk rinforzato dal bordo è in grado di riprodurre il modo in cui la conoscenza cresce nella scienza moderna.
Il professor Vito Latora ha aggiunto:"Il quadro che presentiamo costituisce un nuovo approccio per lo studio dei processi di scoperta, in particolare quelli per i quali la rete sottostante può essere ricostruita direttamente da dati empirici, ad esempio gli utenti che ascoltano musica su una rete di similarità tra i brani. Stiamo già lavorando a questa idea, insieme ad una versione estesa del nostro modello, dove studiamo l'esplorazione collettiva di questi spazi in rete considerando più camminatori contemporaneamente".