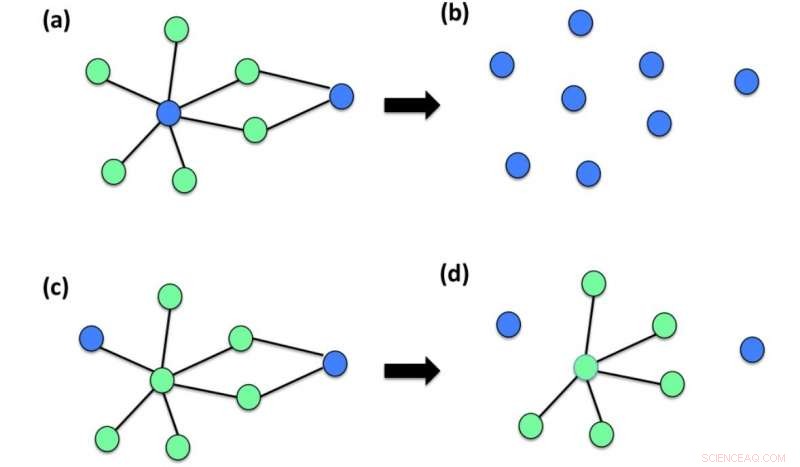
Diverse realizzazioni del danno iniziale sono qui mostrate come più o meno dannose per una rete. Il riquadro (a) mostra un danno iniziale di una rete connessa che interessa esclusivamente due degli N =8 nodi della rete (il nodo blu indica i nodi danneggiati i nodi verdi indicano i nodi non danneggiati). Il pannello (b) mostra che questo danno iniziale è molto dirompente per la rete e risulta in una componente gigante di dimensione R =1. Il pannello (c) mostra un'altra configurazione di danno iniziale della stessa rete che interessa solo due nodi della rete. In questo caso il pannello (d) mostra che l'effetto del danno è ridotto e la maggior parte della rete rimane connessa determinando una componente gigante R =6. Credit:Ginestra Bianconi
Un quadro teorico che spieghi il rischio che eventi rari causino gravi interruzioni in reti complesse, come un blackout in una rete elettrica, è stato proposto da un matematico della Queen Mary University di Londra.
Gli eventi rari possono smantellare bruscamente una rete con conseguenze molto più gravi del solito e comprendere la loro probabilità è essenziale per ridurre le possibilità che si verifichino.
Una rete è formata da un insieme di nodi e dai collegamenti tra di essi. Ad esempio le reti elettriche sono reti i cui nodi sono centrali elettriche collegate dalla rete elettrica. Allo stesso modo una rete ecologica, cui il quadro potrebbe essere applicato, è formato da specie collegate da interazioni ecologiche come una relazione predatore-preda.
Di solito se alcuni dei nodi sono danneggiati, reti come queste sono abbastanza robuste da rimanere funzionali, ma in rare occasioni danni specifici possono portare allo smantellamento dell'intera rete e causare gravi blackout o cambiamenti di regime ecologico, come un collasso ecologico.
I matematici usano spesso la teoria della percolazione, una branca ben sviluppata della matematica applicata che studia la risposta di una rete al danno di una frazione casuale dei suoi nodi, far luce su questi fenomeni. Però, questa teoria è in grado solo di caratterizzare la risposta media di una rete al danno casuale. Pertanto la previsione del comportamento medio non può essere utilizzata per stimare il rischio di collasso della rete a seguito di un evento raro.
Questo studio stabilisce una teoria della percolazione a grande deviazione che caratterizza la risposta di una rete a eventi rari. Il quadro teorico proposto cattura correttamente l'effetto delle configurazioni di danni rari che possono essere osservati nelle reti reali. È interessante notare che il lavoro rivela che le transizioni di percolazione discontinue - bruschi collassi di una rete - si verificano non appena vengono presi in considerazione eventi rari.
Il quadro teorico potrebbe consentire lo sviluppo di strategie per sostenere le reti identificando quali nodi devono essere preservati per prevenire un collasso.
Ginestra Bianconi, autore dello studio, ha dichiarato:"C'è urgente necessità di valutare il rischio di collasso in risposta a rare configurazioni di danno iniziale. Questo risultato mette in luce la fragilità nascosta delle reti e il loro rischio di crollo improvviso e potrebbe essere particolarmente utile per comprendere i meccanismi per evitare il catastrofico smantellamento delle reti reali".
Ha aggiunto:“È importante stimare il rischio di una drammatica cascata di guasti perché si vuole ridurre il rischio. Nella progettazione di una rete elettrica che deve fornire energia a un intero Paese si vogliono evitare rari eventi in cui hai grossi blackout, o nella progettazione di strategie di conservazione di un ecosistema attualmente diversificato e prospero si vuole sapere qual è la probabilità di un improvviso collasso ecologico ed estinzione di massa. Pertanto è necessario comprendere questo rischio che questi eventi accadano".
Il presente studio di grande deviazione della percolazione considera esclusivamente la percolazione di nodi su singole reti come quelle menzionate. Però, Ginestra Bianconi suggerisce che la metodologia delineata potrebbe essere estesa allo studio di modelli più dettagliati di propagazione dei guasti degli eventi.