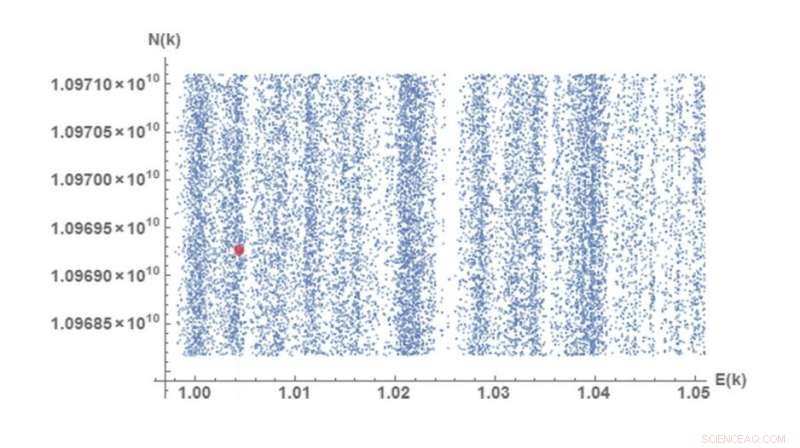
Questo grafico di valori nell'insieme di fattorizzazione di 10, 000 mostra che i valori sono correlati allo spettro di banda di un sistema quantistico. Il punto rosso segna un esempio:il punto N =10, 969, 262, 131 =47, 297x231, 923, E =1.00441815 (dove Ek è una funzione descritta nell'articolo). Credito:Rosales e Martin. ©2018 American Physical Society
Scomporre numeri molto grandi nei loro "mattoni" principali è estremamente difficile per i computer classici, e questa difficoltà è alla base della sicurezza di molti algoritmi crittografici. Mentre è facile scomporre il numero 20 come prodotto dei primi 2 x 2 x 5, Per esempio, fattorizzare numeri più grandi diventa esponenzialmente più difficile quando si utilizzano algoritmi di fattorizzazione classici.
In un nuovo articolo pubblicato su Revisione fisica A , i fisici Jose Luis Rosales e Vicente Martin hanno sviluppato un metodo che può rendere molto più facile scomporre in fattori numeri molto grandi che sono noti per avere esattamente due fattori primi. Il nuovo metodo determina la probabilità che un qualsiasi numero primo sia uno dei due fattori primi di un dato numero. Dopo aver determinato queste probabilità, i candidati a fattore primo più probabili possono essere testati per primi, consentendo di identificare i fattori primi molto più rapidamente di prima.
"La teoria mostra non solo dove si trovano i numeri primi, ma anche la probabilità che un numero primo sia un fattore di un dato numero, "Rosales ha detto Phys.org . "Certo, questo ha implicazioni nella crittografia perché [il crittosistema] RSA ignora questa regolarità."
Una delle cose interessanti del nuovo metodo è che non usa nessun tipo di computer, classico o quantistico. Si tratta invece di un sistema quantistico fisico - un "simulatore quantistico" - che, quando codificato con il numero da scomporre, mostra una distribuzione di probabilità dei valori energetici equivalente alla distribuzione di probabilità dei candidati fattori primi del numero codificato.
"Il nostro obiettivo è sviluppare una nuova teoria quantistica del problema della fattorizzazione utilizzando un simulatore quantistico, " Ha detto Rosales. "Il nostro approccio ha scoperto una proprietà senza alcuna analogia classica nella teoria dei numeri. Ogni coppia di numeri primi che risolve il problema si riorganizza per formare uno schema regolare:lo spettro di banda del simulatore quantistico".
L'idea generale alla base del simulatore quantistico è qualcosa chiamato "insieme di fattorizzazione, " che i ricercatori hanno introdotto in precedenza. Si basa sull'idea che i numeri primi siano ordinati dal minore al maggiore (ad esempio, 2 è il primo numero primo, 3 è il secondo primo, e 101 è il 26 ns primo). È anche possibile prendere la radice quadrata di qualsiasi numero, e poi confronta il risultato con il primo più vicino. Per esempio, la radice quadrata di 27 è poco più di 5, che è il terzo primo. Per definizione di insieme di fattorizzazione, ciò significa che 27 appartiene all'insieme di fattorizzazione di 3.
I fisici hanno quindi dimostrato di poter trasformare la funzione di insieme di fattorizzazione in una funzione della fisica quantistica (la funzione dell'oscillatore armonico invertito). Dopo molti altri passaggi, alla fine hanno mostrato che lo spettro energetico previsto di un sistema quantistico corrisponde alla distribuzione dei numeri primi nell'insieme di fattorizzazione di un numero. Da queste informazioni, i ricercatori possono determinare la probabilità che un numero primo sia un fattore di quel numero. Per verificare la validità del loro metodo, i fisici hanno testato alcuni numeri e confrontato i loro risultati con le distribuzioni effettive ottenute utilizzando le tavole dei numeri primi, e ho trovato distribuzioni molto simili.
I fisici hanno teoricamente dimostrato che il simulatore quantistico proposto può fattorizzare numeri che sono molti ordini di grandezza più grandi di quelli che sono stati fattorizzati con i computer quantistici. Nella loro carta, riportano i risultati dell'uso del loro metodo per determinare la distribuzione di probabilità dei fattori primi di un numero con 24 cifre. Ulteriore, il metodo lo fa con molte meno risorse di quelle richieste dai classici algoritmi di fattorizzazione.
"Nella teoria quantistica, la complessità algoritmica è solo polinomiale con il numero di bit del numero da fattorizzare, " Disse Rosales. "In effetti, i nostri primi risultati sembrano confermare che il simulatore richiede solo (log√N) 3 stati quantistici per riprodurre il suo spettro di energie, un risultato molto incoraggiante».
Un ultimo punto di interesse è che il nuovo metodo ha forti connessioni con l'ipotesi di Riemann, quale, se è vero, suggerirebbe che i numeri primi sono distribuiti in modo prevedibile, allo stesso modo della distribuzione degli zeri della funzione Riemann-zeta. Dimostrare (o confutare) l'ipotesi di Riemann è uno dei più grandi problemi irrisolti in matematica, e uno dei problemi del Millennium Prize del Clay Mathematics Institute.
"I numeri primi dovrebbero comportarsi come numeri quantici se si applica la congettura di Hilbert-Polya, "Rosali ha detto, riferendosi all'approccio di lunga data per dimostrare l'ipotesi di Riemann.
Andando avanti, i ricercatori stanno attualmente lavorando all'implementazione sperimentale del simulatore quantistico utilizzando due particelle entangled in una trappola di Penning.
"Il trattamento completamente quantistico del simulatore richiederebbe un'analisi ottica quantistica delle interazioni dei fotoni con due (o più) ioni entangled in una trappola di Penning, " Rosales ha detto. "Questa parte del programma è ancora in fase di sviluppo. L'obiettivo è costruire sperimentalmente un simulatore di fattorizzazione quantistica. Se implementato con successo, numeri di molti ordini di grandezza maggiori di quelli disponibili per la sua elaborazione quantistica utilizzando l'algoritmo di Shor saranno fattorizzati e, come sottoprodotto, la congettura di Hilbert-Polya sarà testata sperimentalmente."
© 2018 Phys.org