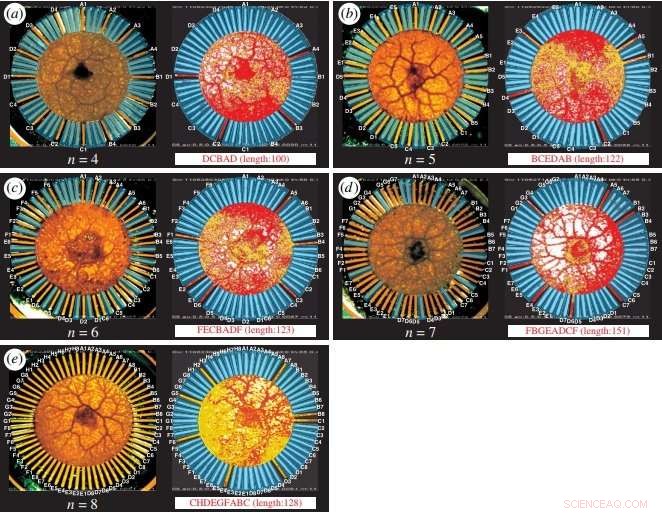
Soluzioni TSP ottenute dal sistema informatico basato su ameba per 4, 5, 6, 7, e 8 città. Credito:Zhu et al. ©2018 Royal Society Open Science
I ricercatori hanno dimostrato che un'ameba, un organismo unicellulare costituito principalmente da protoplasma gelatinoso, ha capacità di calcolo uniche che potrebbero un giorno offrire un'alternativa competitiva ai metodi utilizzati dai computer convenzionali.
I ricercatori, guidato da Masashi Aono alla Keio University, assegnato un'ameba per risolvere il problema del commesso viaggiatore (TSP). Il TSP è un problema di ottimizzazione in cui l'obiettivo è trovare il percorso più breve tra più città, in modo che ogni città venga visitata esattamente una volta, e il punto iniziale e quello finale sono gli stessi.
Il problema è NP-difficile, il che significa che all'aumentare del numero di città, il tempo necessario a un computer per risolverlo cresce in modo esponenziale. La complessità è dovuta al gran numero di possibili soluzioni. Per esempio, per quattro città, ci sono solo tre percorsi possibili. Ma per otto città, il numero di percorsi possibili sale a 2520.
Nel nuovo studio, i ricercatori hanno scoperto che un'ameba può trovare soluzioni ragionevoli (quasi ottimali) al TSP in un lasso di tempo che cresce solo linearmente all'aumentare del numero di città da quattro a otto. Sebbene i computer convenzionali possano anche trovare soluzioni approssimate in tempo lineare, l'approccio dell'ameba è completamente diverso dagli algoritmi tradizionali. Come spiegano gli scienziati, l'ameba esplora lo spazio della soluzione ridistribuendo continuamente il gel nel suo corpo amorfo a velocità costante, nonché elaborando il feedback ottico in parallelo anziché in serie.
Sebbene un computer convenzionale possa ancora risolvere il TSP molto più velocemente di un'ameba, soprattutto per problemi di piccole dimensioni, i nuovi risultati sono intriganti e possono portare allo sviluppo di nuovi computer analogici che derivano soluzioni approssimate di problemi computazionalmente complessi di dimensioni molto più grandi in tempo lineare.
Come funziona
Il particolare tipo di ameba utilizzato dagli scienziati era un plasmodio o "vera muffa melmosa, " che pesa circa 12 mg e consuma fiocchi d'avena. Questa ameba deforma continuamente il suo corpo amorfo fornendo e prelevando ripetutamente gel a una velocità di circa 1 mm/secondo per creare appendici simili a pseudopodi.
Nei loro esperimenti, i ricercatori hanno posizionato l'ameba al centro di un chip stellato, che è un piatto rotondo con 64 canali stretti che si proiettano verso l'esterno, e poi messo il chip sopra una piastra di agar. L'ameba è confinata all'interno del chip, ma può ancora passare ai 64 canali.
Per massimizzare l'assorbimento dei nutrienti, l'ameba cerca di espandersi all'interno del chip per entrare in contatto con quanto più agar possibile. Però, l'ameba non ama la luce. Poiché ogni canale può essere illuminato selettivamente dalla luce, è possibile costringere l'ameba a ritirarsi dai canali illuminati.
Per modellare il TSP, ogni canale nel chip stellato rappresenta una città ordinata nel percorso del venditore. Per esempio, nel caso di quattro città etichettate A-D, se l'ameba occupa i canali A4, B2, C1, e D3, quindi la soluzione corrispondente al TSP è C, B, D, UN, C.
Per guidare l'ameba verso una soluzione ottimale o quasi ottimale, la chiave sta nel controllare la luce. Per fare questo, i ricercatori utilizzano un modello di rete neurale in cui ogni sei secondi il sistema aggiorna quali canali sono illuminati. Il modello incorpora informazioni sulla distanza tra ciascuna coppia di città, così come il feedback dalla posizione attuale dell'ameba nei canali.
Il modello assicura che l'ameba trovi una valida soluzione al TSP in alcuni modi. Per esempio, una volta che l'ameba ha occupato una certa frazione di un particolare canale, diciamo A3, poi i canali A1, A2, e tutti gli altri canali "A" sono illuminati per impedire che la città A venga visitata due volte. Anche, B3, C3, D3, e tutti gli altri "3" canali sono illuminati per vietare le visite simultanee a più città.
Il modello tiene conto delle distanze tra le città rendendo più semplice l'illuminazione dei canali che rappresentano città con distanze maggiori rispetto a distanze minori. Ad esempio, diciamo che l'ameba occupa il canale B2, e ha iniziato a invadere i canali C3 e D3 in egual misura, e la distanza tra le città B e C è 100 mentre la distanza tra le città B e D è 50. La distanza maggiore tra B e C fa sì che il sistema alla fine illumini il canale C3, facendo ritirare l'ameba da quel canale ma permettendole di continuare a muoversi in D3.
Globale, modellare il TSP con un'ameba sfrutta la naturale tendenza dell'ameba a cercare un equilibrio stabile. Poiché i canali che rappresentano percorsi più brevi hanno meno probabilità di essere illuminati, l'ameba può espandersi in quei canali e continuare ad esplorare altri canali non illuminati per massimizzare la sua superficie sulla piastra di agar.
I ricercatori hanno anche sviluppato una simulazione al computer chiamata AmoebaTSP che imita alcune delle caratteristiche principali di come l'ameba affronta il problema, compreso il movimento continuo di gel in quanto viene fornito a velocità costante e prelevato da vari canali.
"Nel nostro chip stellare per risolvere il n -città TSP, l'area totale del corpo dell'ameba diventa n quando l'ameba trova finalmente una soluzione approssimativa, "Aono ha detto Phys.org . "Sembra esserci una 'legge' secondo cui l'ameba fornisce la sua risorsa gelatinosa per espandersi nei canali non illuminati a un ritmo costante, dire, X . Questa legge verrebbe mantenuta anche quando alcune risorse si riprendessero dai canali illuminati. Quindi il tempo necessario per espandere l'area del corpo n per rappresentare la soluzione diventa n / X . Questo meccanismo sarebbe l'origine del tempo lineare, ed è stato riprodotto dal nostro modello di simulazione al computer.
"Ma ancora, il meccanismo attraverso il quale come l'ameba mantiene la qualità della soluzione approssimata, questo è, la breve lunghezza del percorso, resta un mistero. Sembra che la chiave siano i movimenti spazialmente e temporalmente correlati delle parti ramificate dell'ameba situate in canali distanti. Ciascuno di questi rami fa oscillare il suo volume con qualche 'memoria' temporale su esperienze illuminate. I gruppi dei rami eseguono la sincronizzazione e la desincronizzazione per condividere le informazioni anche se spazialmente distanti."
Nel futuro, i ricercatori hanno in programma di migliorare ulteriormente le capacità di calcolo dell'ameba.
"Indagheremo ulteriormente come queste complesse dinamiche oscillatorie spazio-temporali migliorano le prestazioni computazionali nel trovare soluzioni di qualità superiore in tempi più brevi, ", ha affermato il coautore Song-Ju Kim della Keio University. "Se potesse essere chiarito, la conoscenza contribuirà a creare nuovi computer analogici che sfruttino le dinamiche spazio-temporali della corrente elettrica nel suo circuito.
"Certo, eseguendo altri algoritmi su computer digitali tradizionali per il tempo lineare, possiamo derivare soluzioni approssimate a TSP. D'altra parte, quando eseguiamo i nostri modelli di simulazione (AmoebaTSP o le sue versioni sviluppate) sui computer tradizionali come abbiamo fatto in questo studio, le dinamiche spazio-temporali analogiche e parallele richiedono tempi non lineari per simularle come processi digitali e seriali. Quindi stiamo cercando di ottenere soluzioni di qualità molto più elevata rispetto a quelle derivate da quelle tradizionali eseguendo i nostri modelli su computer analogici per un tempo lineare o più breve".
I ricercatori si aspettano anche che, fabbricando un chip più grande, l'ameba sarà in grado di risolvere i problemi di TSP con centinaia di città, anche se ciò richiederebbe decine di migliaia di canali.
© 2018 Science X Network