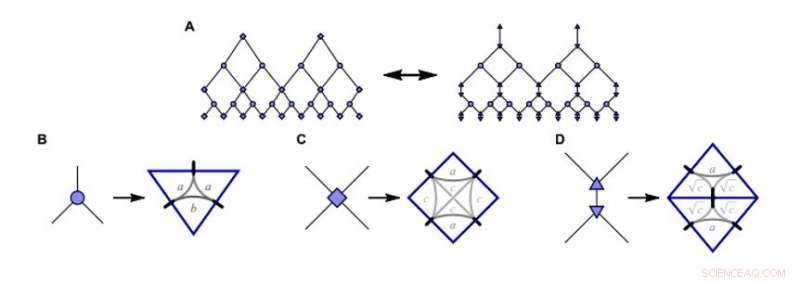
Costruzione del modello giocattolo matchgate MERA (simulazione di ansatz di rinormalizzazione dell'entanglement multiscala; mMERA). A:La rete tensoriale MERA standard (a sinistra) nell'impostazione del matchgate numerico dello studio è equivalente a B-D:Isometrie, districatori, e districatori triangolati (da sinistra a destra) espressi come tensori matchgate. I parametri liberi a, B, c fissare i componenti delle matrici generatrici. Credito:progressi scientifici, doi:10.1126/sciadv.aaw0092
Le reti di tensori assumono un ruolo centrale nella fisica quantistica in quanto possono fornire un'approssimazione efficiente a classi specifiche di stati quantistici. Il linguaggio grafico associato può anche facilmente descrivere e ragionare pittoricamente sui circuiti quantistici, canali, protocolli e sistemi aperti. In un recente studio, A. Jahn e un gruppo di ricerca nei dipartimenti di sistemi quantistici complessi, materiali ed energia e matematica e informatica in Germania hanno introdotto un quadro versatile ed efficiente per studiare le reti di tensori estendendo gli strumenti precedenti. I ricercatori hanno utilizzato la piastrellatura di massa (tecnica geometrica informatica) nel loro lavoro per ottenere dati critici altamente accurati e hanno stabilito un collegamento tra i codici di correzione degli errori quantistici olografici e le reti di tensori. Si aspettano che il lavoro stimoli ulteriori indagini sui modelli di rete tensoriale per catturare le corrispondenze bulk-bounder. I risultati sono ora pubblicati su Progressi scientifici .
La corrispondenza AdS/CFT, che sta per corrispondenza anti-de Sitter/teoria di campo conforme, è una delle più vaste aree di ricerca nella teoria delle stringhe, ed è un esempio nel contesto delle dualità bulk-boundary in cui esiste una dualità olografica tra gravità in uno spazio bulk e un campo quantistico critico sul suo confine. Questa corrispondenza che mette in relazione due teorie molto diverse è stata originariamente formulata dal fisico Juan M. Maldacena nel 1997, ed è considerato un risultato significativamente importante nella teoria delle stringhe negli ultimi 20 anni.
Una caratteristica chiave di queste dualità è la relazione tra la geometria bulk e le entropie dell'entanglement di confine, che i fisici avevano precedentemente illuminato utilizzando la formula Ryu-Takayanagi. Poiché è importante comprendere l'entanglement nel contesto di AdS/CFT, i ricercatori si sono resi conto della necessità delle reti tensoriali come struttura ideale per costruire modelli giocattolo olografici, come la simulazione di ansatz di rinormalizzazione dell'entanglement multiscala (MERA). I fisici avevano precedentemente esplorato la realizzazione che la correzione dell'errore quantistico potrebbe essere facilitata da una dualità olografica, che si collegava ulteriormente alle idee della teoria dell'informazione quantistica. Sebbene i ricercatori siano riusciti a costruire diversi modelli di reti tensoriali per riprodurre una varietà di aspetti su AdS/CFT, mancavano ancora di una comprensione generale delle caratteristiche e dei limiti dell'olografia della rete tensoriale. Gli ostacoli specifici al processo includono gli spazi dei parametri potenzialmente grandi delle reti tensoriali e i notevoli costi computazionali coinvolti.
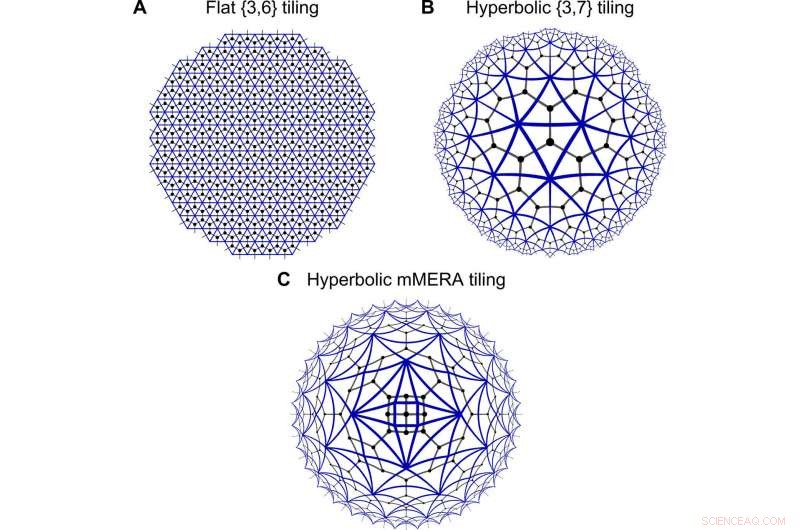
Geometrie di reti tensoriali. Discretizzazioni dello spazio piatto (A) e iperbolico (B e C) con una piastrellatura triangolare (bordi blu), in cui è incorporata una rete tensoriale (reticolo nero). Nel formalismo matchgate, i bordi congiunti tra i triangoli corrispondono a un'integrazione su una coppia di numeri di Grassmann, analogo alla contrazione della rete tensoriale sugli indici. Mentre (A) e (B) mostrano tasselli regolari, (C) presenta una piastrellatura non regolare tipo MERA, che gli scienziati hanno chiamato matchgate MERA (mMERA). Credito:progressi scientifici, doi:10.1126/sciadv.aaw0092
Nel presente lavoro, Jahn et al. ha superato le sfide esistenti applicando tecniche di contrazione altamente efficienti sviluppate da tensori matchgate. Le tecniche versatili hanno permesso al team di ricerca di studiare in modo completo l'interazione tra geometria e correlazioni nelle reti tensoriali fermioniche gaussiane incorporando modelli giocattolo di correzione degli errori quantistici. Hanno anche incluso precedenti approcci alla rete di tensori come il modello "MERA" all'interno del presente lavoro, per evidenziare le connessioni tra di loro. Il team ha limitato lo studio a reti tensoriali non unitarie e reali, simile a un'evoluzione euclidea dalla massa al confine. Jahn et al. fornito nuovi approcci nel contesto della rinormalizzazione della rete tensoriale, per dimostrare la capacità delle reti tensoriali di descrivere le corrispondenze bulk-boundary al di là dei modelli noti. Il presente lavoro è preliminare e fornisce un punto di partenza per studi più sistematici sull'olografia nelle reti tensoriali.
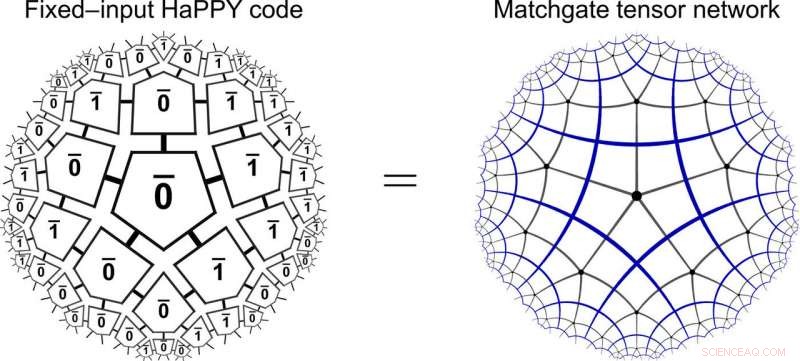
Equivalenza HaPPY/matchgate. Il codice del pentagono olografico del modello HaPPY per l'input bulk computazionale fisso (a sinistra) è uguale a una rete di tensori matchgate su una piastrellatura del pentagono iperbolico (a destra). Credito:progressi scientifici, doi:10.1126/sciadv.aaw0092
Gli scienziati hanno prima applicato la loro struttura alla classe altamente simmetrica di regolari tassellature di massa per implementare il codice olografico di correzione degli errori (codice HaPPY) proposto altrove. Successivamente, hanno esplorato la versatilità del framework per estenderlo verso configurazioni più fisiche. Hanno utilizzato per la prima volta il modello di codice giocattolo HaPPY per comprendere la corrispondenza massa/confine con la piastrellatura di massa dei pentagoni olografici, dove ogni riquadro del pentagono codificava un qubit logico a tolleranza d'errore. Brevemente, il team di ricerca ha osservato che fissare i gradi di libertà di massa agli stati della base computazionale potrebbe dar luogo a una rete di tensori matchgate. Hanno mostrato che gli stati della base computazionale sono gaussiani puri e hanno concluso che per input computazionali fissi nella massa, il codice del pentagramma olografico potrebbe produrre un tensore matchgate sul confine. Usando un simbolo Schläfli {p, q} dove p =il numero di spigoli per poligono e q =il numero di poligoni attorno a ciascun angolo, hanno specificato la geometria iperbolica del modello HaPPY.
Dopo Jahn et al. hanno mostrato la loro struttura del modello per includere il codice del pentagono olografico costruito da stati stabilizzatori a cinque qubit per input bulk fissi. Hanno mostrato che gli stati limite corrispondono all'accoppiamento di massa non locale con particelle esotiche note come fermioni di Majorana. Il lavoro ha così aperto la strada allo studio delle proprietà di stato di un modello olografico di grandi dimensioni. Gli scienziati hanno inoltre calcolato i correlatori a due punti e le entropie di entanglement del sistema. Hanno quindi dimostrato che gli stati limite gaussiani critici e con gap possono essere realizzati al di là dei modelli noti utilizzando vari tasselli di massa. Nel presente lavoro hanno riprodotto le proprietà di scalatura media del modello giocattolo Ising CFT (conformal field theory); modello più semplice possibile in fisica teorica che ha permesso i metodi della teoria quantistica euclidea dei campi e lo studio dei fenomeni critici.
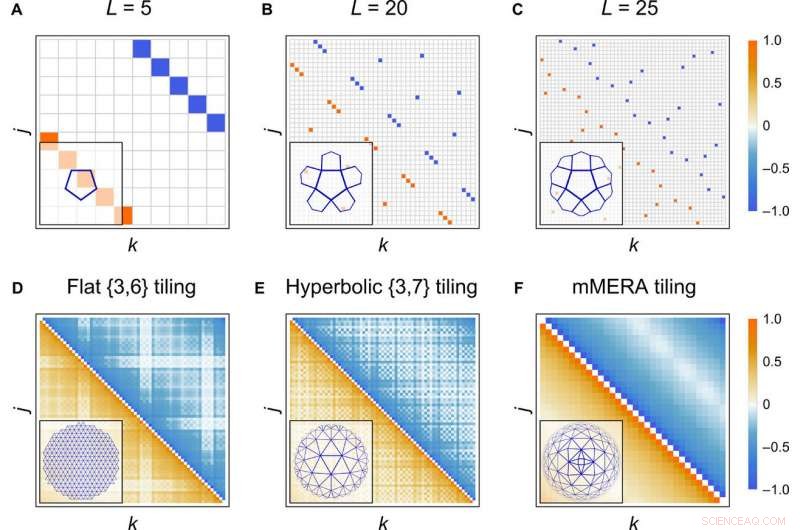
Correlazioni allo stato limite. (da A a C) Matrice di covarianza di Majorana Γ con voci codificate per colore per uno stato al contorno di un'iperbolica {5, 4} affiancamento del codice HaPPY con input fisso 0¯ su ogni tessera. Il confine è costituito da 2L =10, 40, e 50 siti Majorana, rispettivamente. (D a F) Matrice di correlazione di campo 〈ψjψk − ψkψj〉/2 =(Γ2j, 2k−1 + Γ2j−1, 2k)/4 per gli stati limite del {3, 6}, {3, 7}, e piastrellatura mMERA a criticità con L =63, 69, e 64 siti di confine, rispettivamente. Le voci della matrice sono normalizzate alla stessa scala di colori. La piastrellatura corrispondente a ciascuna matrice di correlazione in (A) a (F) è mostrata nell'angolo in basso a sinistra. Credito:progressi scientifici, doi:10.1126/sciadv.aaw0092
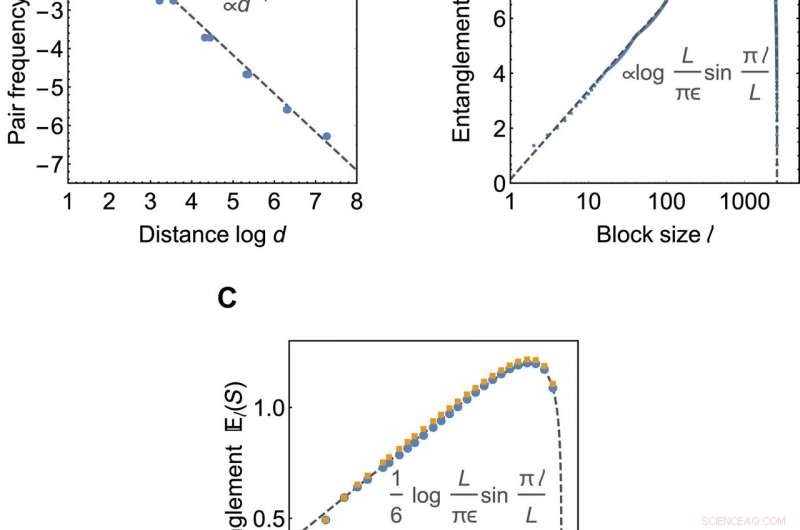
Correlazioni critiche e scala di entanglement. (A e B) Proprietà dello stato limite del codice HaPPY in 2605 siti di confine. (A) mostra le correlazioni medie alla distanza di confine d, calcolata come frequenza relativa n di coppie di Majorana. La linea grigia tratteggiata mostra un adattamento numerico n(d)~1/d. (B) mostra la scala dell'entropia di entanglement medio El(S) con la dimensione del sottosistema l. La linea grigia tratteggiata mostra l'adattamento numerico utilizzando (11). (C) El(S) per piastrellature regolari ai valori critici a =0,580 per a {3, 6} piastrellatura (blu) e a =0.609 per {3, 7} affiancamento (giallo) con 348 siti di confine ciascuno. La linea grigia tratteggiata mostra l'esatta soluzione c =1/2 CFT. Credito:progressi scientifici, doi:10.1126/sciadv.aaw0092
Jahn et al. ha quindi costruito una rete tensoriale euclidea matchgate basata sulla geometria MERA precedentemente sviluppata e l'ha chiamata matchgate MERA (mMERA). Questa invarianza di piastrellatura che hanno espresso come una triangolazione (misure multiple per catturare un costrutto), recuperato il CFT di Ising con poco costo computazionale. Il processo di ottimizzazione computazionale nello studio ha richiesto solo pochi minuti su un computer desktop per una rete con centinaia di tensori.
In questo modo, A. Jahn e colleghi hanno introdotto un quadro preliminare efficiente per studiare le reti tensoriali e hanno proposto ulteriori studi all'interno dell'impostazione gaussiana per concentrarsi su volumi curvati positivamente, modelli dimensionali superiori e tensori casuali. Ulteriori studi oltre la gaussianietà potrebbero esplorare le reti di tensori fermionici interagenti mediante espansione di accoppiamento debole o con interazioni localmente limitate. Entrambe le possibili estensioni suggerite del quadro presentate nello studio richiederanno solo il polinomio di scala computazionale alla dimensione del sistema per evitare sforzi computazionali proibitivi dei metodi generali per estrarre la contrazione del tensore.
© 2019 Scienza X Rete