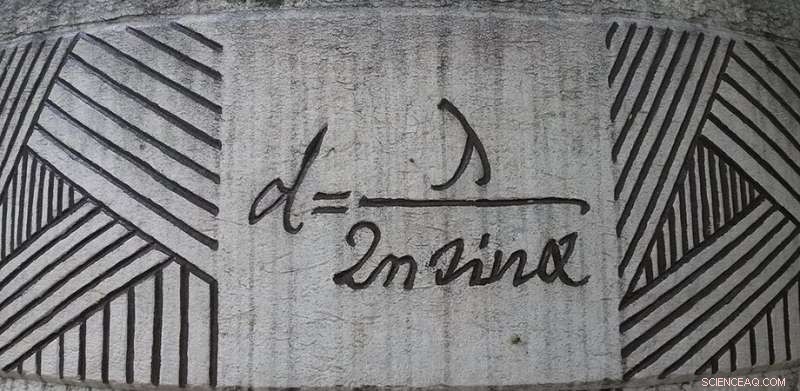
L'equazione di diffrazione di Ernst Abbe in mostra a Jena, Germania. Credito:Daniel Mietchen, Wikimedia, commons.wikimedia.org/wiki/File:Ernst-Abbe-Denkmal_Jena_F%C3%BCrstengraben_-_20140802_125709.jpg
Anche se ci è stato detto che un'immagine parla più di mille parole, quel luogo comune sottovaluta seriamente il valore di una buona immagine. La nostra comprensione di come funziona il mondo è semplificata dalla nostra capacità di trasformare i dati in immagini. L'immagine è al centro della scienza:se può essere misurata, verrà trasformato in un'immagine da analizzare.
Il fattore limitante dell'imaging è la risoluzione. Quanto possono essere vicini due oggetti prima che un sistema di imaging li riduca in un unico punto sfocato? A questa domanda fu inizialmente risposto da Ernst Abbe nel 1873. Egli teorizzò che se due oggetti sono più vicini di circa metà lunghezza d'onda, non possono essere risolti. Abbe ha ottenuto il suo limite considerando come la diffrazione di una lente offusca una sorgente puntiforme.
Da circa un secolo, Il limite di diffrazione di Abbe fu preso come una verità scientifica. Sicuro, potresti giocare con la luce illuminante e il mezzo di imaging per ottenere un fattore di due o tre, ma fattori di dieci o 100 erano inconcepibili. Che ora è cambiato, con molte tecniche di imaging in grado di risolvere oltre il limite di diffrazione di Abbe, che ora giace in frantumi nell'angolo dell'officina della scienza all'ombra di due premi Nobel. Ma c'è ancora un limite? Quanto possono essere vicini due oggetti prima che si confondano in un unico punto? Questa è la domanda a cui Evgenii Narimanov della Purdue University ha cercato di rispondere in un recente Fotonica avanzata carta.
Immagini sfocate
Quando si tratta di immagini, è molto più semplice mettere da parte il concetto di diffrazione e pensare invece all'informazione. Quando un oggetto viene ripreso, la luce viene diffusa dall'oggetto verso il sistema di imaging. Il modello spaziale, o informazioni, dell'immagine è trasportata dalle frequenze spaziali della luce. Per recuperare un'immagine accurata, il sistema di imaging deve trasmettere quelle frequenze spaziali senza modificarle. Ma, ogni sistema ha i suoi limiti, quindi il contributo di alcune frequenze spaziali andrà perso.
L'immagine risultante è realizzata ricombinando le frequenze spaziali trasmesse dal sistema di imaging. Se il sistema di imaging non è in grado di trasmettere frequenze al di sopra di un certo limite, quindi l'immagine non conterrà tali informazioni, con conseguente sfocatura. Se si considera il sistema di imaging in grado di trasmettere frequenze spaziali fino a una frequenza di taglio, ma incapace di trasmettere frequenze al di sopra del limite, quindi la risoluzione dell'immagine risultante sarà esattamente quella prevista da Abbe (ma con una matematica più semplice).
Infatti, le informazioni trasmesse da un sistema di imaging sono descritte esattamente dalla stessa matematica utilizzata dagli ingegneri che studiano la trasmissione dei dati lungo i cavi telefonici, che consente di utilizzare gli strumenti della teoria dell'informazione per prevedere le prestazioni dei sistemi di imaging.
Decodificare i messaggi in un'immagine
Narimanov ha fatto un ulteriore passo avanti nell'astrarre il processo di imaging considerando solo il trasferimento di informazioni, indipendentemente da come tale informazione è codificata. Quando ciò è fatto, la risoluzione di un'immagine è determinata solo dalle informazioni reciproche condivise tra l'oggetto e l'immagine. In questo quadro, che è indipendente da tutti i dettagli funzionali, il limite di risoluzione è dato dal rumore introdotto durante il trasferimento delle informazioni. In pratica il rumore è dovuto al rilevatore, dispersione di luce, fluttuazioni delle condizioni di illuminazione, e molti altri dettagli.
Adottando questo approccio astratto, Narimanov è stato in grado di produrre una teoria che prevede la migliore risoluzione possibile per un'immagine basata solo sul rapporto tra l'intensità del segnale e la quantità di rumore. Maggiore è il rapporto segnale-rumore, migliore è la risoluzione possibile.
Sfruttando questa teoria, il documento include anche una serie di calcoli per sistemi di imaging più specifici, come quelli che utilizzano l'illuminazione strutturata, e nel caso dell'imaging di oggetti sparsi, che hanno poche caratteristiche spesso raggruppate insieme. Vengono discusse anche le possibilità di migliorare un'immagine con la post-elaborazione:tutti conosciamo i polizieschi televisivi che sembrano in grado di migliorare le immagini a piacimento. Sebbene ciò non sia possibile come mostrato in TV, c'è un elemento di verità. Metodi validi per la postelaborazione computazionale di un'immagine possono rivelare alcuni dettagli nascosti. Questa teoria mostra i limiti di tale approccio, pure.
L'approccio di Narimanov non rivela quale aspetto di un sistema attualmente limiti la risoluzione. Per quello, sono ancora necessari modelli più specifici. Anziché, è meglio pensare al modello di Narimanov come una guida:dove si trovano i maggiori guadagni di risoluzione con il minimo sforzo? Queste informazioni sono utili per decidere dove investire tempo e denaro.