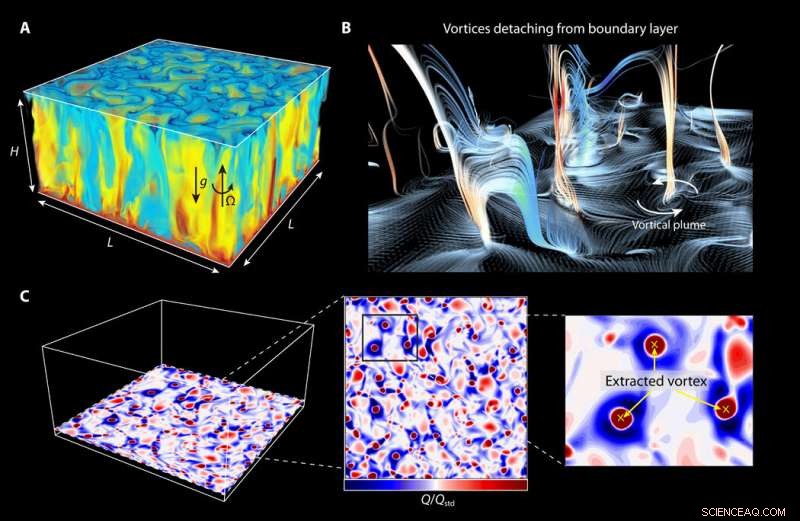
Strutture di flusso con rotazione. Istantanee delle linee di flusso (A) della temperatura e (B) provenienti dallo strato limite termico inferiore. (C) Istantanee di Q/Qstd (criterio Q) scattate orizzontalmente al bordo dello strato limite termico per numero di Ekman (Ek) =4 × 10-5 e Ra =108 e una dimostrazione del vortice estratto. Le posizioni del centro del vortice sono contrassegnate da croci gialle. Credito:progressi scientifici, doi:10.1126/sciadv.aaz1110
Il moto browniano delle particelle nel fluido è un comportamento collettivo comune nei sistemi biologici e fisici. In un nuovo rapporto su Progressi scientifici , Kai Leong Chong, e un team di ricercatori in fisica, ingegneria, e ingegneria aerospaziale in Cina, ha condotto esperimenti e simulazioni numeriche per mostrare come il movimento dei vortici assomigliasse alle particelle Browniane inerziali. Durante gli esperimenti, il flusso vorticoso convettivo turbolento rotante ha permesso alle particelle di muoversi balisticamente all'inizio e diffusivamente dopo un momento critico in una transizione comportamentale diretta, senza passare attraverso un regime di memoria idrodinamica. Il lavoro implica che i vortici convettivi hanno una memoria indotta dall'inerzia, così il loro movimento a breve termine è stato qui ben definito nel quadro del moto browniano per la prima volta.
moto browniano
Albert Einstein fornì per la prima volta una spiegazione teorica al moto browniano nel 1905 con il movimento delle particelle di polline in un bagno termale, il fenomeno è ormai un comune esempio di processi stocastici che si verificano ampiamente in natura. Più tardi nel 1908, Paul Langevin notò l'inerzia delle particelle e predisse che il loro movimento sarebbe stato balistico entro un breve periodo di tempo, passare al movimento diffuso dopo una linea temporale specifica. Però, data la rapidità di questo passaggio, ci è voluto più di un secolo perché i ricercatori potessero osservare direttamente il fenomeno. Tuttavia, il moto browniano "puro" previsto da Langevin non è stato osservato nei sistemi liquidi e la transizione ha attraversato un'ampia gamma di scale temporali. La transizione lenta e graduale si è verificata a causa dell'effetto memoria idrodinamica, per generare infine correlazioni a lungo raggio. Gli scienziati avevano precedentemente osservato l'effetto della memoria idrodinamica in più sistemi, comprese le sospensioni colloidali, particelle sospese nell'aria e particelle intrappolate in pinzette ottiche. In questo lavoro, Chong et al. ha mostrato come i vortici in flussi altamente connettivi si comportassero come particelle inerziali per eseguire puro moto browniano, per la prima volta, senza essere influenzato dall'effetto idrodinamico. Hanno identificato ed estratto i vortici utilizzando il criterio Q (un metodo per l'identificazione dei vortici). Il lavoro li aiuterà a prevedere il movimento del vortice durante un periodo di tempo specifico nei sistemi astrofisici e geofisici.
Moto da balistico a diffusivo di vortici convettivi. (A) Il MSD dei vortici in funzione del tempo. (B) MSD normalizzato in funzione di t/tc. La linea continua rappresenta un fit dell'Eq. 4 ai dati. Sia in (A) che (B), i simboli solidi denotano risultati numerici a Ra =1 × 108, ei simboli aperti denotano risultati sperimentali a Ra =3 × 107. (C) Coefficiente di diffusione D dei vortici (simboli aperti) e la scala temporale caratteristica tc per la transizione del moto (simboli solidi) in funzione Ra/Rac. (D) Funzione di autocorrelazione della velocità (VACF) rispetto a t/tc per diversi Ek. La linea tratteggiata rappresenta C(t)=2Dtcexp(−t/tc). La linea continua indica un decadimento della legge di potenza per il VACF (i dati per t ≳ 5tc hanno qualche dispersione a causa di statistiche insufficienti). Si noti che tutte le quantità fisiche sono rese adimensionali come descritto nel testo principale. Credito:progressi scientifici, doi:10.1126/sciadv.aaz1110 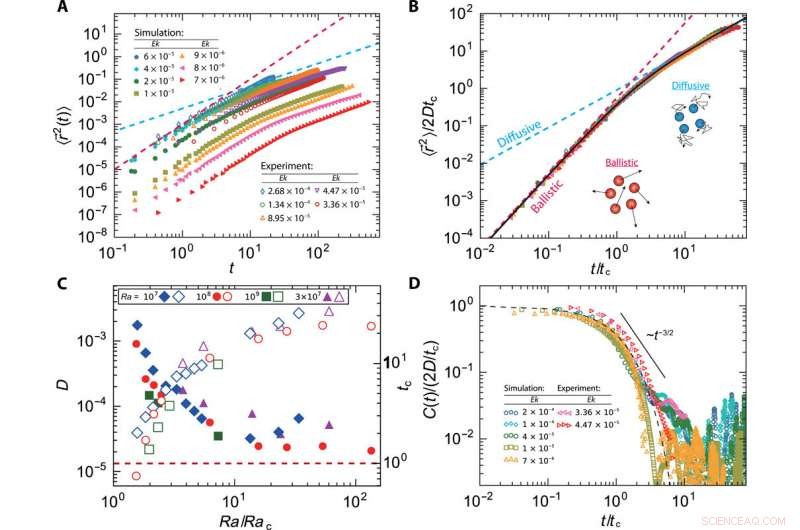
Una sfida esistente nella ricerca astrofisica e geofisica consiste nel prevedere il movimento dei vortici entro un determinato periodo di tempo. Chong et al. ha utilizzato un sistema modello per studiare i vortici nei flussi convettivi noto come convezione di Rayleigh Benard (RB), che include uno strato fluido di altezza fissa, riscaldato dal basso e raffreddato dall'alto, mentre viene ruotato attorno all'asse verticale con una velocità angolare. La differenza di temperatura nel sistema ha destabilizzato il flusso affinché si verificasse la convezione quando l'azionamento termico era sufficientemente forte. Gli scienziati hanno utilizzato tre parametri adimensionali per caratterizzare la dinamica del flusso, compreso il numero di Rayleigh (Ra), Numero di Prandtl (Pr) e numero di Ekman (Ek). In presenza di rotazione, strutture vorticose sono emerse come particelle fluide che si muovevano a spirale verso l'alto o verso il basso. I ricercatori continuano a studiare questi pennacchi vorticosi a causa della loro importanza nel trasporto di quantità di moto e di calore.
Chong et al. per primo ha studiato il movimento dei vortici tracciando il loro cambiamento di posizione tramite una serie di istantanee. Hanno caratterizzato il comportamento statistico dei vortici utilizzando il loro spostamento quadratico medio (MSD). I valori MSD per diversi Ek e Ra hanno mostrato un comportamento simile indicando che in un breve lasso di tempo il movimento del vortice si è trasferito dal movimento balistico al movimento diffusivo. Questa transizione assomigliava al moto browniano in un bagno termale. Gli scienziati hanno quindi trattato i vortici come particelle Browniane e hanno descritto il loro movimento risolvendo l'equazione di Langevin per ottenere il loro MSD. I risultati hanno implicato dinamiche simili del movimento del vortice per Ra ed Ek, suggerendo che i vortici mostrassero un comportamento "puro browniano". Nel sistema di convezione, i vortici trasportavano pacchi fluidi che erano più caldi e più freddi del fluido circostante; questa differenza di densità relativamente piccola causata dalle variazioni di temperatura nell'esperimento ha dato origine al notevole comportamento balistico.
Vortici che formano un reticolo con una velocità di rotazione sufficientemente elevata. (A) Istantanee di Q/Qstd scattate orizzontalmente al bordo dello strato limite termico per, da sinistra a destra, Ek =4 × 10−5, 1 × 10-5, e 7 × 10−6 a Ra =108. (B) Funzione di distribuzione radiale g(r) in funzione di r/a, dove a è il raggio medio dei vortici. (C) Il valore massimo gmax della funzione di distribuzione radiale rispetto a Ra/Rac (il caso di Ra =3 × 107 è dall'esperimento, gli altri provengono da DNS). Credito:progressi scientifici, doi:10.1126/sciadv.aaz1110 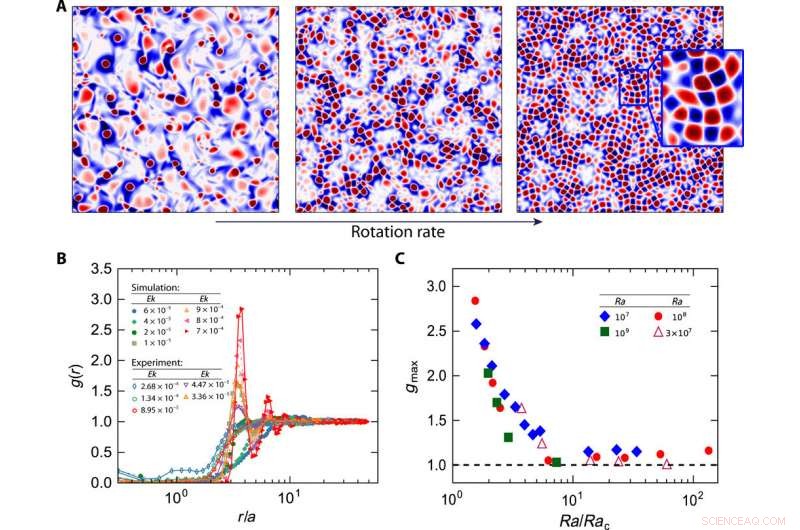
Nonostante il moto browniano, la distribuzione spaziale dei vortici non era casuale, ed esibito strutture modellate, che gli scienziati hanno ottenuto utilizzando istantanee di diversi tassi di rotazione. Al variare del numero di Ekman (Ek), diversi cambiamenti si sono verificati nella distribuzione dei vortici. All'inizio, il numero di vortici aumenta con la velocità di rotazione, in modo che i vortici inizialmente diluiti e distribuiti casualmente diventassero altamente concentrati e raggruppati. L'aumento della densità del numero di vortici con la velocità di rotazione concordava anche con le indagini precedenti. Prossimo, quando la velocità di rotazione diventa sufficientemente alta, formavano una struttura a griglia di vortice. Quando Chong et al. ingrandito in una regione locale per osservare il più alto tasso di rotazione, hanno osservato uno schema regolare per tali strutture a griglia di vortice. Le regioni rossastre dei vortici hanno formato un reticolo quadrato e le regioni localizzate bluastre intermedie hanno mostrato un comportamento ad alta deformazione. Il team ha attribuito i modelli quadrati osservati nel lavoro a diverse impostazioni dei confini e parametri di controllo.
Nonostante il movimento casuale nel dominio temporale, i vortici mostravano uno specifico ordine spaziale, che ha portato a un'apparente contraddizione. Chong et al. osservato le traiettorie dei vortici durante la rotazione lenta e veloce. Però, i vortici non viaggiavano abbastanza lontano da "vedere" o interagire con altri vortici. Hanno attribuito l'ordine spaziale dei vortici alla competizione tra i due processi dinamici caratterizzati dalla scala temporale di rilassamento del vortice e dalla scala temporale browniana, rispettivamente.
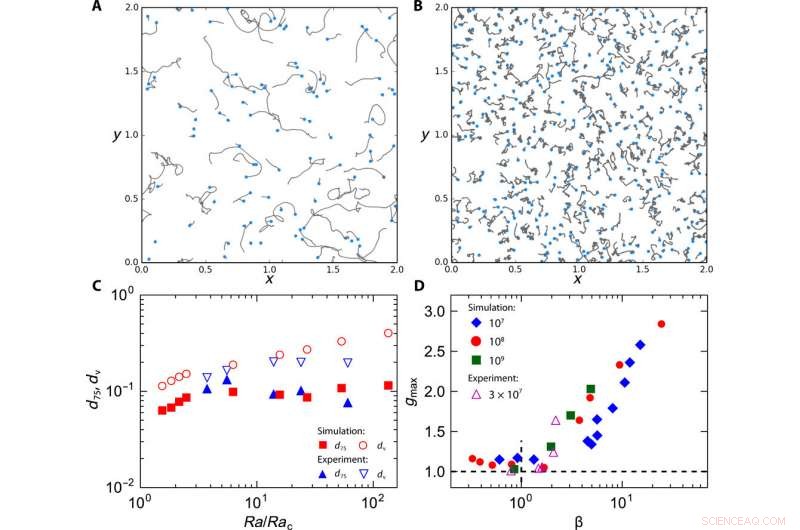
Moto localizzato dei vortici. Traiettorie dei vortici:(A) Ek =1 × 10−4 e (B) Ek =7 × 10−6; in entrambi i casi, Ra =1 × 108. I punti blu indicano la fine delle traiettorie. (C) La distanza media (dv) tra i vortici (simboli aperti) e il 75° percentile della distanza (d75) percorsa dai vortici (simboli pieni), in funzione di Ra/Rac per Ra =1 × 108 (simulazione, simboli rossi) e Ra =3 × 107 (esperimento, simboli blu). (D) La funzione di distribuzione radiale massima gmax versus definita come il rapporto tra la scala temporale Browniana e la scala temporale di rilassamento. Credito:progressi scientifici, doi:10.1126/sciadv.aaz1110
In questo modo, Kai Leong Chong e colleghi hanno mostrato come il movimento dei vortici nella convezione termica rotante assomigliasse alle particelle inerziali che eseguono il movimento browniano. Il movimento ha subito una brusca transizione da regioni balistiche a regioni diffusive senza sperimentare una regione di memoria idrodinamica intermedia. L'osservazione del moto browniano puro fu predetta per la prima volta da Paul Langevin, sebbene non sia stato precedentemente osservato nella pratica per le particelle inerziali nei sistemi liquidi. Il lavoro ha evidenziato il lavoro teorico classico esistente che ha mostrato come le tracce passive esibissero una transizione dal comportamento balistico a quello diffusivo, simile alle osservazioni sperimentali di questo studio. Il moto browniano puro osservato indicava anche l'insignificanza dell'effetto memoria idrodinamica. Chong et al. considerata la forza di Coriolis durante lo studio per la sua rilevanza nella formazione di vortici nei fenomeni naturali, compresi i cicloni tropicali nell'atmosfera, vortici oceanici e la longeva macchia rossa gigante su Giove. I risultati influenzeranno molte situazioni in astrofisica, geofisica e meteorologia.
© 2020 Scienza X Rete