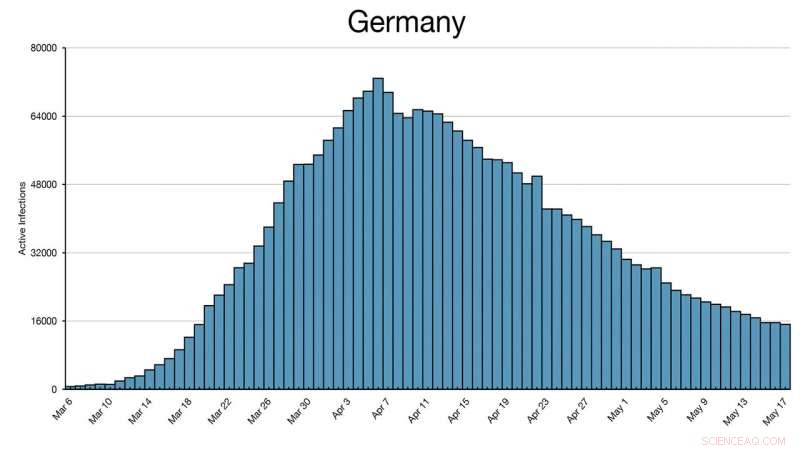
Questo istogramma della Germania mostra che ha raggiunto il picco il 4/6/20 e in parte è stato riaperto ad aprile. Il confine con l'Austria è rimasto chiuso tranne che per il pendolarismo di lavoro. Le frontiere sono state riaperte il 15/6/20, ma le maschere sono state indossate nelle aziende tedesche fino a luglio. La Germania non è scesa al livello del 16/03/20 fino al 10/06/20, quasi tre mesi dopo. Credito:Joseph Lee McCauley
Durante i primi mesi della pandemia di COVID-19, Joseph Lee McCauley, professore di fisica all'Università di Houston, stava guardando i dati giornalieri per sei paesi e si chiedeva se le infezioni stessero davvero crescendo in modo esponenziale. Estraendo dai dati i tempi di raddoppio, si convinse che lo erano.
Tempi di raddoppio e crescita esponenziale vanno di pari passo, quindi gli è diventato chiaro che la modellazione basata su infezioni passate è impossibile, perché il tasso cambia imprevedibilmente di giorno in giorno a causa del distanziamento sociale e degli sforzi di blocco. E le variazioni dei tassi differiscono per ciascun paese in base all'entità del distanziamento sociale.
In I progressi dell'AIP , McCauley spiega come ha combinato la matematica nella forma della disuguaglianza di Tchebychev con un insieme statistico per capire come la crescita esponenziale macroscopica con diversi tassi giornalieri derivi dall'infezione della malattia da persona a persona.
"Equazioni cinetiche chimiche ordinarie discretizzate applicate a infetti, non infetto, e recuperate parti della popolazione mi hanno permesso di organizzare i dati, così ho potuto separare gli effetti del distanziamento sociale e dei recuperi all'interno dei tassi di infezione giornalieri, "Ha detto McCauley.
Il plateau senza picco si verifica se il tasso di recupero è troppo basso, e gli Stati Uniti, UK., e la Svezia rientrano in quella categoria. Le equazioni non possono essere ripetute per guardare al futuro, perché il tasso di domani è sconosciuto finché non si dispiega.
"I modellisti tendono ad applicare erroneamente le equazioni chimico cinetiche come SIR (Susceptible, infettivo, o Recuperato) o SEIR (Suscettibile, Esposto, infettivo, o Recuperato) modelli, perché stanno cercando di generare tassi futuri da tassi passati, " ha detto McCauley. "Ma il passato non ti permette di usare equazioni per prevedere il futuro in una pandemia, perché il distanziamento sociale cambia le tariffe ogni giorno".
McCauley ha scoperto di poter fare una previsione in cinque secondi tramite un calcolatore manuale che è buono come qualsiasi modello di computer semplicemente utilizzando i tassi di infezione per oggi e ieri.
"Il lockdown e il distanziamento sociale lavorano, " disse McCauley. "Confronta l'Austria, Germania, Taiwan, Danimarca, Finlandia, e molti altri paesi che hanno raggiunto il picco all'inizio di aprile, con gli USA, UK., Svezia, e altri senza blocco o blocchi svogliati:non si sono mai nemmeno stabilizzati, molto meno a picco".
Sottolinea che le previsioni non possono prevedere un picco o addirittura un plateau. Il plateau non implica il picco, e se si verifica un picco, non c'è nulla nei dati per mostrare quando accadrà. Succede quando il tasso di guarigione è maggiore del tasso di nuove infezioni.
"Il distanziamento sociale e i blocchi riducono il tasso di infezione ma non possono causare picchi, "Ha detto McCauley. "Distanziamento sociale e recuperi sono due termini separati all'interno delle equazioni del tasso cinetico giornaliero".
L'implicazione di questo lavoro è che il denaro per la ricerca potrebbe essere speso meglio rispetto a costosi modelli epidemici.
"I politici dovrebbero conoscere abbastanza aritmetica per ricevere istruzioni sulle implicazioni, "Ha detto McCauley. "L'effetto dei blocchi e del distanziamento sociale si manifesta nei tempi di raddoppio osservati, e c'è anche un tempo di raddoppio previsto basato su due giorni, che serve come una buona previsione per il futuro."