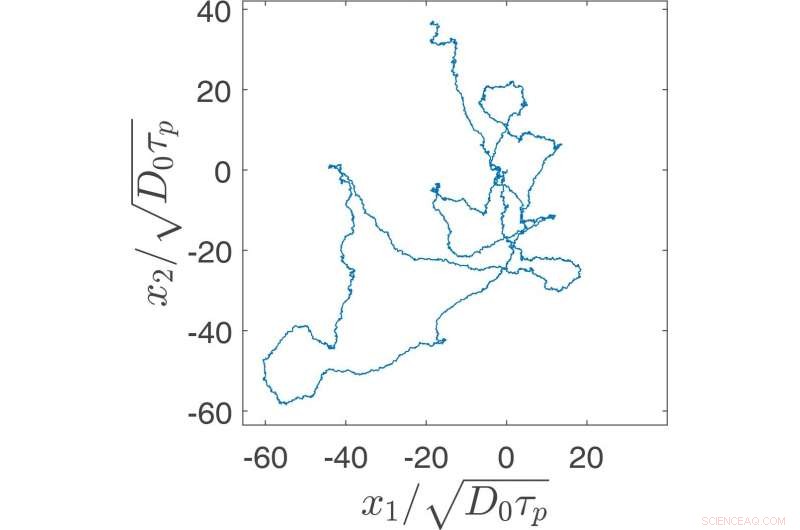
Deviazione dal moto browniano. Credito:SciencePOD
In circostanze normali, le particelle seguiranno movimenti casuali ben stabiliti mentre si diffondono attraverso liquidi e gas. Eppure in alcuni tipi di sistema, questo comportamento può essere interrotto, il che significa che i movimenti di diffusione delle particelle non sono più influenzati dai risultati delle catene di eventi precedenti. Attraverso una ricerca pubblicata in EPJ MI , Bernhard Mitterwallner, un dottorato di ricerca studente nel team di Roland Netz presso la Libera Università di Berlino, Germania, ha sviluppato nuove teorie che descrivono in dettaglio come queste dinamiche insolite possono essere riprodotte in modelli matematici generalizzati.
L'approccio del team potrebbe consentire ai ricercatori di saperne di più sui comportamenti, compreso il trasporto di cellule biologiche, ei movimenti dei materiali "attivi", le cui particelle raccolgono energia negli ambienti circostanti per spingersi in avanti. Tipicamente, queste caratteristiche di diffusione appaiono solo brevemente come sistemi di transizione tra stati stabili, ma nelle giuste condizioni, possono persistere per tempi molto più lunghi. I ricercatori possono studiare questo effetto introducendo un "termine di memoria" nei loro calcoli, che possono spiegare le influenze degli eventi passati su scale temporali diverse. Diversi studi hanno ora utilizzato questo principio per esplorare come questo "movimento transitorio persistente" può essere catturato in modelli di mezzi viscoelastici, che possono resistere alla deformazione quando viene applicato lo stress.
Gli autori hanno adottato un approccio più generale nel loro studio; basando i loro calcoli su un'equazione del moto che offrisse un quadro utile per descrivere comportamenti di diffusione non convenzionali. Quando si aggiunge un termine di memoria nell'equazione, i loro modelli danno luogo a movimenti transitori persistenti in una gamma di sistemi diversi, che non era stato esplorato in studi precedenti. I risultati del team potrebbero ora consentire ai ricercatori di modellare accuratamente i comportamenti di diffusione in una gamma più ampia di situazioni e potrebbero essere particolarmente utili per gli studi di materiali avanzati che rispondono all'ambiente circostante.