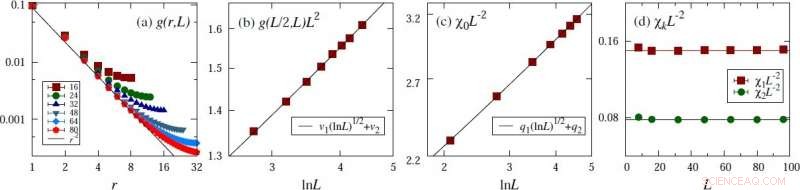
Prove per la forma di ridimensionamento ipotizzata nell'esempio del modello critico 4D XY. (a) Funzione di correlazione a due punti. (b) Correlazione a due punti alla distanza della metà della dimensione del sistema lineare. (c) Suscettività magnetica. (d) Fluttuazioni magnetiche in modi di Fourier diversi da zero. Credito:©Science China Press
Dall'istituzione della teoria dei gruppi di rinormalizzazione, è noto che i sistemi di fenomeni critici possiedono tipicamente una dimensione critica superiore dc (dc=4 per il modello O(n)), tale che in dimensioni spaziali pari o superiori a dc, il comportamento termodinamico è governato da esponenti critici che assumono valori di campo medio. Contrariamente alla semplicità del comportamento termodinamico, la teoria dello scaling a dimensione finita (FSS) per d> dc O(n) era sorprendentemente sottile ed era rimasto oggetto di dibattito in corso fino a poco tempo fa, quando è stato ipotizzato un ansatz di scala a due lunghezze per la funzione di correlazione a due punti, numericamente confermato, e in parte supportato da calcoli analitici.
Alla dimensionalità critica superiore dc, le correzioni logaritmiche moltiplicative e additive generalmente si verificano al comportamento del campo medio nudo. Il chiarimento delle correzioni logaritmiche in FSS diventa "notoriamente difficile, ' a causa della mancanza di approfondimenti analitici oltre il livello fenomenologico e del limite delle dimensioni dei sistemi disponibili nelle simulazioni numeriche. La precisa forma logaritmica FSS a d=dc è rimasta un problema di vecchia data.
Recentemente, Jian-Ping Lv, Wanwan Xu, e Yanan Sun dell'Anhui Normal University, Kun Chen di Rutgers, l'Università statale del New Jersey, e Youjin Deng della University of Science and Technology of China e della Minjiang University hanno affrontato l'FSS logaritmico della simmetria O(n) alla dimensionalità critica superiore. Prendendo in prestito intuizioni da dimensioni superiori, hanno stabilito una forma di scala esplicita per la densità di energia libera, che consiste contemporaneamente in un termine di scala per il punto fisso gaussiano e un altro termine con correzioni logaritmiche moltiplicative. In particolare, hanno ipotizzato che la correlazione critica a due punti di dimensione finita mostri un comportamento a due lunghezze, che è governato dal punto fisso gaussiano a distanza minore, ed entra in un plateau a una distanza maggiore la cui altezza diminuisce con la dimensione del sistema in una legge di potenza corretta da un esponente logaritmico.
Su questa base, sono state previste le FSS di varie grandezze macroscopiche. Hanno quindi effettuato ampie simulazioni Monte Carlo per il modello di n-vettori con n=1, 2, 3, e ottenuto solide prove a sostegno delle forme di ridimensionamento ipotizzate dall'FSS della suscettibilità, le fluttuazioni magnetiche nei modi di Fourier diversi da zero, il raccoglitore cumulativo, così come la correlazione a due punti alla distanza della metà della dimensione del sistema lineare. Questo è un passo significativo verso una soluzione completa dell'FSS logaritmico a d=dc per sistemi con dimensionalità critica superiore.
Lo studio non è solo di importanza teorica nei sistemi modello, ma anche di rilevanza pratica per un gran numero di sistemi sperimentali. Si noti che, a causa degli sviluppi tecnologici, la realizzazione sperimentale del modello O(n) è ora disponibile in vari sistemi fisici tra cui materiali magnetici quantistici, array di giunzione Josephson, e sistemi atomici ultrafreddi. Secondo la mappatura quantistica-classica, i sistemi O(n) quantistici tridimensionali sono alla dimensionalità critica superiore.