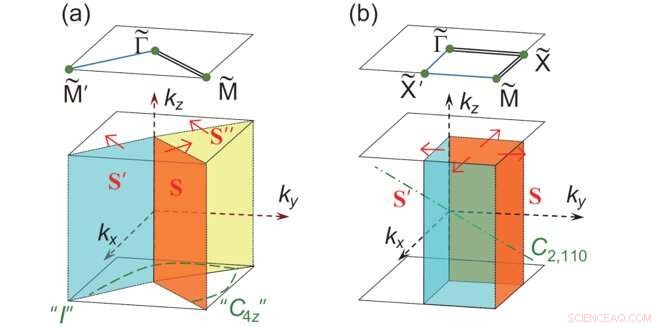
La definizione di in sistemi con simmetria S4 sulla superficie arancione S. Il sistema in (b) ha C2, 110 simmetria. Credito:Science China Press
Un nuovo invariante topologico è definito in sistemi con S 4 simmetria per diagnosticare l'esistenza dei fermioni di Weyl. Calcolando , il costo computazionale per la ricerca dei semimetalli Weyl è notevolmente ridotto. Recentemente, Gao et al. ha implementato questo metodo nello screening ad alto rendimento e ha trovato molti nuovi candidati semimetallici Weyl con proprietà esotiche, fornendo piattaforme realistiche per futuri studi sperimentali dell'interazione tra i fermioni di Weyl e altri stati esotici.
Utilizzando le simmetrie dei sistemi, le persone possono definire vari invarianti topologici per descrivere diversi stati topologici. I materiali topologici possono essere scoperti con precisione calcolando gli invarianti topologici. Recentemente, i ricercatori hanno scoperto che le rappresentazioni irriducibili e le relazioni di compatibilità possono essere utilizzate per determinare se un materiale è un isolante topologico non banale/banale (che soddisfa le relazioni di compatibilità) o un semimetallo topologico (che viola le relazioni di compatibilità), che porta a un gran numero di materiali topologici previsti da calcoli teorici.
Però, I semimetalli di Weyl vanno oltre questo paradigma perché l'esistenza dei fermioni di Weyl non necessita di alcuna protezione di simmetria (ad eccezione delle simmetrie di traslazione reticolare). Attualmente, le persone di solito prendono una griglia molto densa nella zona tridimensionale di Brillouin per cercare i fermioni di Weyl con zero band gap. A causa della grande quantità di calcolo richiesta, questo metodo è molto inefficiente. Perciò, non può essere utilizzato per la ricerca ad alto rendimento dei fermioni di Wey. Considerando le enormi potenziali applicazioni dei semimetalli Weyl, è urgente progettare un nuovo algoritmo o definire un nuovo invariante topologico per cercare i fermioni di Weyl in modo accurato e rapido.
In un recente lavoro pubblicato su Bollettino Scientifico , Gao et al. proposto un nuovo invariante topologico in sistemi con S 4 simmetria, che può essere usato per diagnosticare efficacemente l'esistenza dei fermioni di Weyl. Inoltre, per sistemi magnetici, il diverso da zero può essere rivelato dalle rappresentazioni irriducibili degli stati occupati su S 4 k-punti invarianti. Quindi riduce notevolmente il costo di calcolo per la ricerca dei fermioni di Weyl. Vale la pena notare che questo nuovo invariante χ funziona sia per sistemi magnetici che non magnetici.
Applicando questo metodo allo screening ad alto rendimento nei calcoli dei primi principi, gli autori hanno predetto molti nuovi semimetalli Weyl magnetici e non magnetici. Le osservazioni sperimentali hanno dimostrato che questi semimetalli Weyl appena scoperti possiedono molte proprietà uniche, come la magnetoresistenza, superconduttività, e spin vetrosi, ecc. Questi materiali forniscono piattaforme realistiche per futuri studi sperimentali dell'interazione tra i fermioni di Weyl e altri stati esotici.