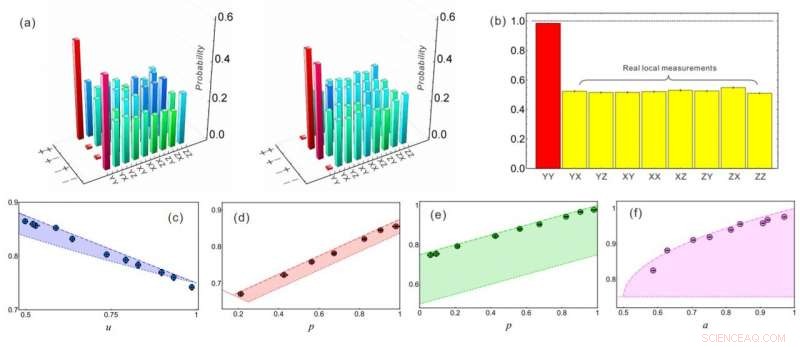
Risultati sperimentali per la discriminazione statale locale. Credito:WU Kangda et al.
Recentemente, un gruppo di ricerca guidato dall'accademico Guo Guangcan del CAS Key Laboratory of Quantum Information dell'Università di Scienza e Tecnologia della Cina (USTC) di CAS, ha compiuto importanti progressi nella teoria dell'informazione quantistica. Il prof. Li Chuanfeng e il prof. Xiang Guoyong del team hanno collaborato con il dott. Strelstov dell'Università di Varsavia per indagare sulla parte immaginaria della teoria quantistica come risorsa, e sono stati ottenuti diversi risultati importanti. I risultati rilevanti sono ora pubblicati congiuntamente come Suggerimenti della redazione in Lettere di revisione fisica e Revisione fisica A .
Un numero complesso è uno strumento matematico, ed è ampiamente usato in meccanica, elettrodinamica, ottica e altri campi correlati della fisica per fornire un'elegante formulazione della teoria corrispondente. La nascita della meccanica quantistica fornisce un'immagine unificata di onde e particelle, e rafforza ulteriormente il ruolo preminente dei numeri complessi in fisica. Però, la questione se le strutture complesse siano necessarie per la meccanica quantistica è stata a lungo dibattuta dai fisici
I ricercatori hanno considerato il numero complesso come una sorta di risorsa quantistica, e rivelare il suo ruolo insostituibile nella discriminazione locale di stati quantistici bipartiti. Per di più, nel quadro della teoria delle risorse quantistiche, hanno studiato il metodo di misurazione di questa risorsa e il problema della trasformazione in varie operazioni libere. Hanno risolto il problema della misurazione della robustezza di dimensioni complesse, trasformazione dello stato quantistico a singolo bit in condizioni di funzionamento libero, e probabilità di mutua trasformazione di qualsiasi stato puro in condizioni di libera operazione.
Utilizzando lo stato entangled a due fotoni preparato mediante conversione parametrica verso il basso, i ricercatori hanno ulteriormente misurato e confrontato la probabilità di successo di distinguere localmente lo stato quantico quando si utilizzava solo la base di misurazione reale e la base di misurazione generale. Hanno osservato con successo l'aumento della probabilità di successo quando si utilizza la base di misurazione complessa, che ha verificato l'importante ruolo del complesso nella meccanica quantistica.
Questo lavoro dimostra che la parte immaginaria è indispensabile nella teoria della meccanica quantistica. Il recensore lo ha altamente raccomandato, notando "Trovo che l'immaginazione quantistica possa essere considerata come una forma più forte di coerenza quantistica... Penso anche che i risultati nel manoscritto stimoleranno la ricerca sui fondamenti quantistici e sulle teorie delle risorse quantistiche con una struttura più ricca."