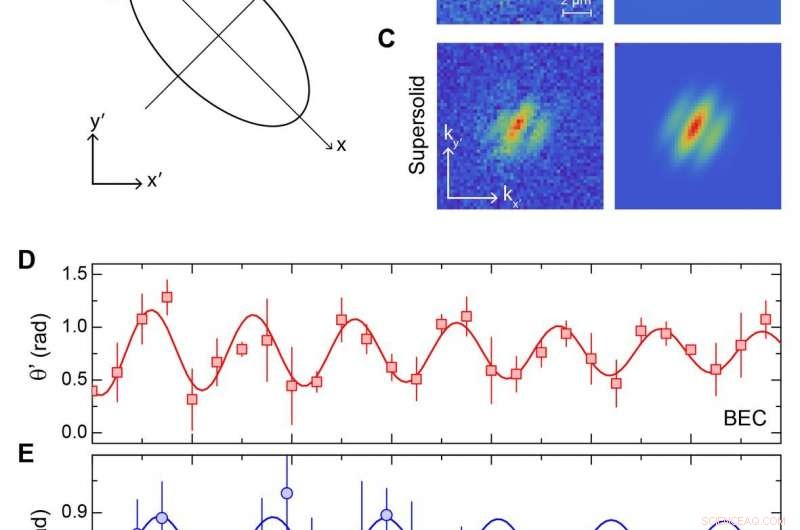
Misure in modalità forbici. A) Schema della geometria sperimentale:il sistema atomico (ellisse) è intrappolato in un potenziale anisotropo con autoassi x e y. Una rotazione improvvisa del potenziale di intrappolamento eccita un'oscillazione angolare θ(t) (frecce rosse). B-C) Esempi delle distribuzioni sperimentali dopo espansione libera e dei corrispondenti accoppiamenti bidimensionali utilizzati per estrarre l'angolo di oscillazione θ 0 dopo l'espansione libera in B) regime BEC (dd=1.14); C) regime supersolido (dd=1,45). D-E). Evoluzione temporale dell'angolo θ 0 (t):D) regime BEC; E) regime supersolido. Le barre di errore rappresentano la deviazione standard di 4-8 misurazioni. Credito:Scienza, doi:10.1126/science.aba4309
La superfluidità nei liquidi e nei gas può manifestarsi come un momento d'inerzia ridotto (l'analogo rotazionale della massa) in caso di rotazioni lente. Effetti rotazionali non classici possono essere considerati anche nelle sfuggenti fasi supersolide della materia in cui la superfluidità può coesistere con una struttura reticolare. In un nuovo rapporto ora pubblicato in Scienza , L. Tanzi e un gruppo di ricerca presso l'Istituto Nazionale di Ottica e il Dipartimento di Astronomia dell'Università di Firenze in Italia, ha mostrato come una fase supersolida scoperta di recente nei gas quantistici dipolari presentasse un momento di inerzia ridotto. Il team ha studiato una peculiare modalità di oscillazione rotazionale in un potenziale armonico per dedurre una frazione supersolida e fornire prove dirette della natura supersolida del costrutto dipolare.
Superfluidi e supersolidità
I superfluidi mostrano le loro proprietà più spettacolari durante la rotazione, dove lo stato superfluido è descritto da una funzione d'onda macroscopica. I fisici avevano già verificato effetti rotazionali non classici per la maggior parte dei superfluidi conosciuti, inclusa la materia nucleare, condensati gassosi di Bose-Einstein e gas di Fermi degeneri. Il risultato è correlato all'effetto Meissner osservato nei superconduttori. Negli anni Sessanta, i ricercatori hanno scoperto un altro tipo di fase bosonica della materia nota come supersolido, descritto da una funzione d'onda macroscopica. In un supersolido, la superfluidità può coesistere con un'architettura di tipo cristallino. Il fisico ha suggerito che il supersolido rotante mostrerebbe un momento di inerzia intermedio a un superfluido e un sistema classico. Questo fenomeno è noto come inerzia rotazionale non classica (NCRI). Queste osservazioni sulla supersolidità sono state fatte principalmente usando elio solido, dove i ricercatori hanno impiegato oscillatori di torsione (sistemi di rotazione) per rilevare NCRI. In questo lavoro, Tanzi et al. ha studiato un diverso candidato supersolido:un condensato gassoso di Bose-Einstein (BEC) di atomi fortemente dipolari.
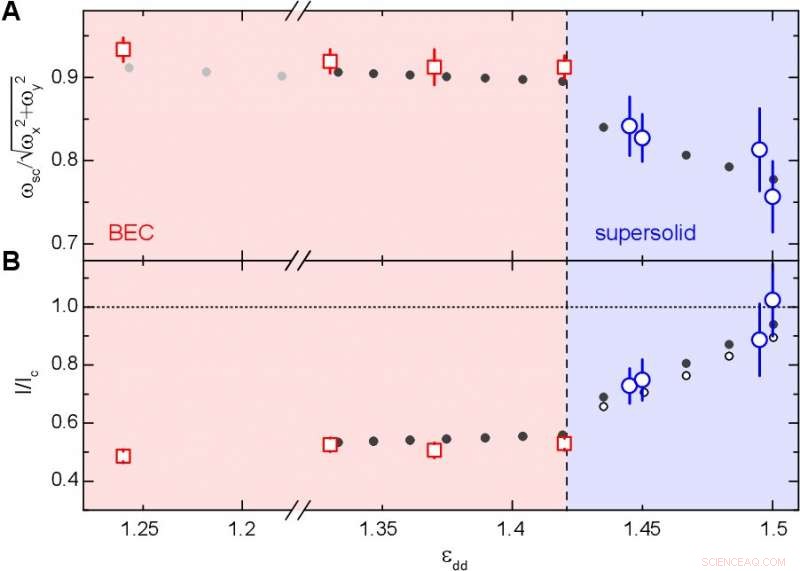
Frequenza e momento d'inerzia della modalità a forbice rispetto al parametro di interazione. A) Frequenze modalità forbici. Grandi cerchi e quadrati sono le misurazioni sperimentali. I diamanti neri e i punti sono le previsioni teoriche del campo medio e oltre il campo medio, rispettivamente. B) Momento d'inerzia. Grandi quadrati e cerchi sono derivati dall'Eq. (1) nello studio, utilizzando le misure sperimentali delle frequenze delle forbici e del teorico; i punti neri sono la simulazione numerica. Piccoli punti aperti sono la previsione teorica per 2. Le barre di errore sono una deviazione standard. L'esperimento ha un'incertezza di calibrazione del 3%. La linea tratteggiata che separa i regimi BEC e supersolido è stata determinata numericamente. Credito:Scienza, doi:10.1126/science.aba4309
I BEC si formano in una frazione sopra lo zero assoluto e solo in atomi che si comportano come bosoni, uno dei due tipi di particelle fondamentali. Quando i bosoni vengono raffreddati a temperature sufficientemente basse, una frazione sostanziale entra spontaneamente in un singolo stato quantistico in un fenomeno noto come condensazione di Bose-Einstein (BEC), e gli esperimenti più famosi sono quelli sui gas atomici. Il sistema quantistico recentemente scoperto ha mostrato un regime modulato in densità che coesiste con la coerenza di fase, come richiesto per la supersolidità. I ricercatori hanno testato la natura dei superfluidi utilizzando modalità di eccitazione non rotazionali relative alle equazioni idrodinamiche per i superfluidi. In linea con i precedenti esperimenti con l'elio, Tanzi et al. focalizzato solo sulla caratterizzazione dell'NCRI (inerzia rotazionale non classica) dei sistemi, al fine di fornire prove dirette di superfluidità in rotazione.
Gli esperimenti
Nella fisica quantistica, È ancora poco pratico ottenere solidi dipolari abbastanza grandi da realizzare una geometria cilindrica. Di conseguenza, i ricercatori hanno selezionato una tecnica di rotazione specifica per adattarsi all'asimmetrico, piccolo sistema in laboratorio. Hanno quindi eccitato la cosiddetta modalità a forbice del sistema; un'oscillazione rotazionale di piccolo angolo del potenziale armonico che contiene naturalmente il sistema. La tecnica è stata precedentemente impiegata per dimostrare la superfluidità nei normali condensati di Bose-Einstein (BEC). Tanzi et al. ha studiato la variazione della frequenza della modalità a forbice durante la transizione dalla forma BEC alla forma supersolida per confrontare direttamente il supersolido con un sistema completamente superfluido. Durante gli esperimenti, il team ha utilizzato un BEC di atomi di disprosio (Dy) fortemente magnetici in una trappola armonica anisotropa con frequenze con i dipoli orientati nella direzione Z tramite un campo magnetico. La temperatura del sistema era sufficientemente bassa e gli scienziati hanno indotto la transizione dal BEC al supersolido sintonizzandosi tramite una risonanza magnetica di Feshbach e le energie di interazione di van der Waals. Gli scienziati si aspettavano che il reticolo fosse composto da un supersolido a grappolo per portare il sistema in un regime di cristalli di goccioline senza coerenza tra le goccioline.
Frazione superfluida da BEC a supersolido. I quadrati rossi e i cerchi blu sono la frazione superfluida dalla frequenza delle forbici misurata sperimentalmente e il teorico, usando l'eq. (3) derivato nello studio. I punti neri sono la frazione superfluida dalla frequenza teorica. I triangoli aperti sono il limite superiore per la frazione superfluida unidimensionale dall'Eq. 4 derivati nello studio. I diamanti sono la frazione superfluida stimata di goccioline indipendenti. Riquadro:la regione grigia è la regione di integrazione per l'Eq. 4 derivati nello studio. Credito:Scienza, doi:10.1126/science.aba4309 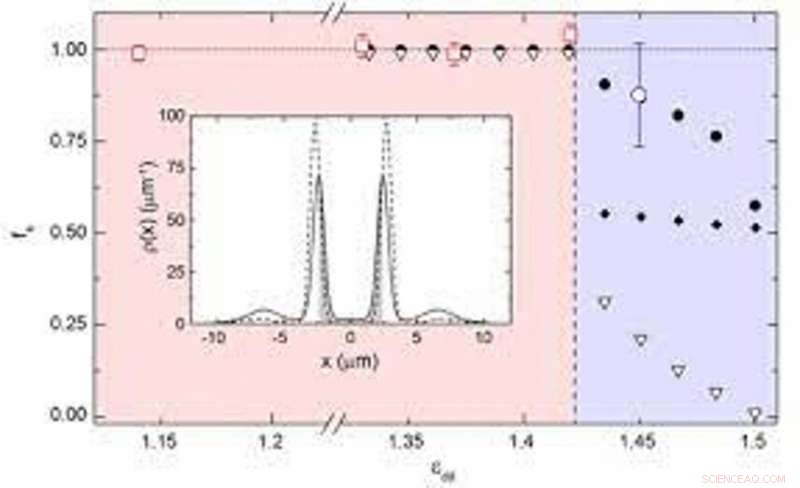
Il team ha quindi eccitato la modalità a forbice e ha calcolato che la frequenza di oscillazione è direttamente correlata al momento di inerzia del superfluido. Hanno quindi collegato il momento d'inerzia a una frazione superfluida specificatamente definita per il sistema. Tanzi et al. ha notato l'analogia della modalità a forbice con gli oscillatori di torsione dell'elio poiché entrambi i sistemi hanno rilevato NCRI (inerzia rotazionale non classica) tramite la frequenza di oscillazione. I risultati sperimentali hanno riassunto le misurazioni delle forbici nei regimi BEC e supersolido. Il team ha ripreso le distribuzioni di densità 2-D dopo un'espansione libera del sistema per rappresentare le distribuzioni di momento efficaci. I regimi BEC e supersolido hanno mostrato oscillazioni a frequenza singola come previsto per i superfluidi che interagiscono debolmente. Per evitare disturbi causati da altre modalità collettive del sistema, Tanzi et al. impiegavano due diverse tecniche di eccitazione per i regimi BEC e supersolido. Hanno quindi ottenuto un riepilogo dei risultati per la frequenza delle forbici e il relativo momento di inerzia e quindi hanno confrontato i risultati con le previsioni teoriche. Il team ha notato una chiara riduzione della frequenza quando il sistema è entrato nel regime supersolido in accordo con la teoria. I risultati hanno fornito ulteriori prove di NCRI per il solido dipolare. Il team ha spiegato i meccanismi mostrati in questo lavoro utilizzando le previsioni originali fatte per la condensazione di Bose nei sistemi di materia condensata.
Veduta
In questo modo, L. Tanzi e colleghi hanno stabilito la natura superfluida del supersolido dipolare caratterizzando la sua inerzia rotazionale non classica. Il supersolido era diverso dai superfluidi standard a causa della frazione superfluida ridotta. La tecnica dettagliata in questo lavoro consentirà ulteriori indagini sui fenomeni in studi futuri. Il team propone di realizzare sistemi più grandi come metodo aggiuntivo per studiare il comportamento dei supersolidi in geometria anulare o in una configurazione 2-D, studiando anche la dinamica dei vortici quantizzati in fase supersolida.
© 2021 Science X Network