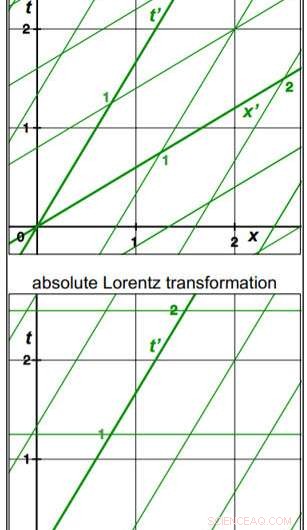
Credito:World Scientific Publishing
Uno degli aspetti strutturali più basilari dello spaziotempo relativistico è la descrizione di come il tempo e le distanze vengono alterati dal movimento. La teoria della relatività speciale descrive una struttura spazio-temporale per il movimento lineare costante in cui il tempo si dilata e le lunghezze si contraggono in risposta al movimento. Questo quadro è descritto dalla trasformazione di Lorentz, che comprende formule matematiche che descrivono come il tempo e la distanza vengono alterati tra i sistemi di riferimento in movimento. La trasformazione di Lorentz descrive anche come un osservatore stazionario vede il tempo nel fotogramma in movimento per essere compensato con la distanza. Lo sfasamento del tempo con la distanza tra i quadri di riferimento genera simultaneità differenziale, in cui eventi che sono simultanei per un osservatore non saranno simultanei per un secondo osservatore in movimento rispetto al primo osservatore.
La natura dello spaziotempo nei frame rotanti non è stata stabilita al livello più fondamentale di definizione della trasformazione che descrive accuratamente gli effetti relativistici e il quadro di simultaneità. In letteratura sono presenti quattro distinte trasformazioni relativistiche rotazionali:la metrica di Langevin; Post trasformazione; trasformazione di Franklin; e la trasformazione assoluta di Lorentz (ALT) nella sua forma rotazionale. Determinare quale trasformazione descrive accuratamente i dati sperimentali indicherebbe la struttura spazio-temporale presente nei fotogrammi rotanti del mondo reale. La comprensione di queste informazioni fondamentali ha un'ampia applicabilità perché la maggior parte della materia visibile nell'Universo è in movimento rotatorio, compresa la Terra rotante.
La trasformazione rotazionale più citata è la metrica di Langevin, descritta per la prima volta nel 1921. Nel corso dei decenni, la metrica di Langevin è stata utilizzata per descrivere la relatività in frame rotanti in centinaia di libri di testo e articoli di ricerca. Però, la metrica di Langevin non è mai stata valutata con dati sperimentali che abbiano una risoluzione sufficiente per distinguerla dalle altre principali trasformazioni rotazionali.
La combinazione di effetti relativistici e simultaneità di una trasformazione influenza il modo in cui la luce si propaga. Le quattro trasformazioni hanno previsioni diverse per le velocità della luce unidirezionali del telaio rotante, velocità della luce a due vie, e l'effetto Sagnac. Questo studio deriva le previsioni ottiche per ogni trasformazione direttamente dalle loro equazioni di trasformazione, con molte delle previsioni non precedentemente riportate in letteratura. Le previsioni vengono quindi confrontate con i recenti dati sperimentali ottici ad alta risoluzione.
I dati del risonatore ottico sulla velocità bidirezionale della luce sono tra le misurazioni scientifiche a più alta risoluzione, con risoluzioni di 10 -18 . Questa alta risoluzione è necessaria per distinguere tra le previsioni delle trasformazioni. Lo studio rivela che ALT e la previsione della trasformazione di Franklin della costante velocità bidirezionale della luce, C, corrisponde ai dati del risonatore ottico, mentre la metrica di Langevin e le previsioni di post trasformazione vengono invalidate dai dati. Il fallimento della metrica di Langevin e della trasformazione Post per far corrispondere i dati del risonatore ottico è dovuto alla loro assenza (o nessuna contrazione netta) della lunghezza nel telaio rotante. In contrasto, le trasformazioni ALT e Franklin mostrano una contrazione della lunghezza, che consente loro previsioni accurate per la velocità bidirezionale della luce.
Dati sull'effetto Sagnac, che ha risoluzioni inferiori di 10 -8 , è compatibile con le previsioni dell'effetto Sagnac della metrica di Langevin, Inviare, e trasformazioni ALT, ma è incompatibile con la trasformazione di Franklin, che non prevede alcun effetto Sagnac. È dimostrato che il fallimento della trasformazione di Franklin nel generare un evidente effetto Sagnac è dovuto alla sua incorporazione della simultaneità differenziale. In contrasto, le altre tre trasformazioni incorporano la simultaneità assoluta in cui il tempo non è compensato dalla distanza, che consente evidenti effetti Sagnac. Così, ALT è l'unica trasformazione che descrive accuratamente l'intera gamma di dati ottici relativistici.
Molteplici pubblicazioni hanno proposto meccanismi per incorporare la simultaneità differenziale nei frame rotanti per consentire la generazione di un evidente effetto Sagnac. Però, questi meccanismi generano equazioni dell'effetto Sagnac alternative. Lo studio mostra che queste equazioni dell'effetto Sagnac alternative implicano velocità della luce bidirezionali invalidate dai dati del risonatore ottico ad alta risoluzione. In contrasto, ALT prevede l'effetto Sagnac convenzionale, che implica la velocità bidirezionale costante della luce, C.
Lo studio dimostra che la trasformazione rotazionale ALT prevede con precisione sia i dati ottici ad alta risoluzione che le osservazioni relativistiche a telaio rotante non ottico. Questa analisi implica che la trasformazione rotazionale ALT descrive la struttura di base dello spaziotempo in frame rotanti. Ciò chiarisce che lo spaziotempo a frame rotante è caratterizzato dagli effetti relativistici della dilatazione del tempo e della contrazione della lunghezza all'interno di un quadro di simultaneità assoluta in cui il tempo non è compensato dalla distanza.