
Un apparato sperimentale per misurare l'effetto Hall convenzionale con campo magnetico perpendicolare alla superficie. Credito:FLEET
Uno studio teorico della FLEET di questa settimana ha trovato una "pistola fumante" nella lunga ricerca del monopolo magnetico topologico denominato curvatura di Berry.
Questa scoperta è una svolta nella ricerca di effetti topologici nei sistemi di non equilibrio.
Il gruppo, guidato da Dimi Culcer all'UNSW, identificato un effetto Hall non convenzionale guidato da un campo magnetico nel piano nei sistemi di fori dei semiconduttori, che è riconducibile esclusivamente alla curvatura di Berry.
(Al contrario, l'effetto Hall ordinario e l'effetto Hall anomalo richiedono entrambi un campo magnetico/magnetizzazione perpendicolare alla superficie.)
Gli effetti topologici potenziati consentirebbero un'elettronica topologica a bassa energia praticabile su larga scala, funzionamento a temperatura ambiente, e sono stati recentemente inclusi nella roadmap IEEE verso l'elettronica del futuro.
La risposta isolante un momento di svolta
"Isolare le risposte topologiche nei 'conduttori regolari' è stato un compito storicamente difficile, " afferma il capo del gruppo di ricerca A/Prof Dimi Culcer (UNSW). "Anche se si ritiene che queste risposte topologiche siano onnipresenti nei solidi".
Risposte quantizzate, come l'effetto Hall quantistico e lo spin-Hall quantistico forniscono una chiara impronta della topologia, tuttavia questi sono stati osservati solo in sistemi unidimensionali (1D) e sono intimamente connessi con l'esistenza di stati limite.
Nei conduttori "normali", significa sistemi 2D e 3D, esiste molta letteratura teorica che prevede contributi topologici ad es. l'anomalo effetto Hall, ma questi non sono mai stati osservati senza ambiguità in una misurazione di trasporto.
Ci sono due ragioni principali per questo:(i) gli elettroni spin-up e spin-down di solito danno contributi opposti, e questi quasi si annullano; (ii) ciò che resta è sopraffatto dal disordine.
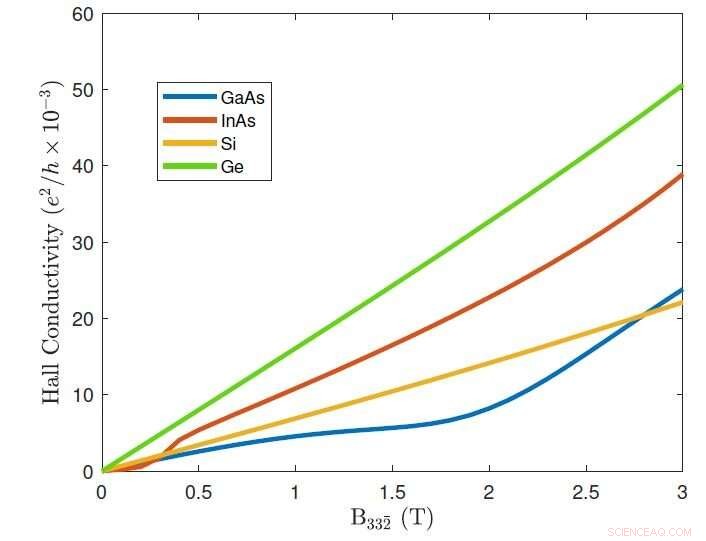
Risposta di conducibilità di Hall al campo magnetico. Credito:FLEET
Il nuovo documento FLEET rimedia a questa lacuna di vecchia data individuando un sistema bidimensionale in cui la curvatura di Berry, e solo la curvatura della bacca, è responsabile del segnale di Hall lineare nel campo magnetico nel piano applicato.
"Sorprendentemente, tutti i contributi di disordine svaniscono:non siamo a conoscenza di nessun altro sistema multidimensionale in cui questo sia vero, "dice l'autore principale, Ph.D. UNSW studente James Cullen. "La sua misurazione sperimentale è accessibile a qualsiasi laboratorio all'avanguardia in tutto il mondo, quindi ci aspettiamo un forte interesse da parte degli sperimentalisti."
Curvatura della bacca, l'effetto Hall anomalo e i materiali topologici
Il team di ricerca ha cercato la traccia matematica rivelatrice chiamata "curvatura della bacca, " che si comprende se si pensa al concetto di trasporto parallelo che compare abitualmente in geometria e relatività generale.
"Pensa a un vettore come a una freccia che posizioniamo da qualche parte sulla superficie di un oggetto solido, " spiega Dimi. "Ora spostiamo la freccia intorno, assicurandosi che punti sempre con lo stesso angolo rispetto alla superficie, questo è infatti come un essere umano che cammina lungo la superficie della Terra. Alla fine riportiamo la freccia al punto di partenza dopo che ha girato intorno, e troviamo che, generalmente, punta in una direzione diversa:ha magicamente ruotato di un certo angolo. La dimensione di questo angolo è determinata dalla curvatura della superficie. "
Nella meccanica quantistica, al posto dei vettori abbiamo funzioni d'onda, ma possiamo descrivere la dinamica usando la stessa immagine, e la curvatura è chiamata curvatura di Berry.
L'angolo di rotazione è sostituito dalla famosa fase Berry, prende il nome dal fisico matematico Prof Sir Michael Berry, che ha formulato il problema negli anni '80. Più tardi, basandosi sul lavoro del premio Nobel David Thouless, Qian Niu di UT Austin ha mostrato che la curvatura di Berry si comporta come l'ambito monopolio magnetico, ma non nello spazio reale, piuttosto nello spazio del momento, che è lo spazio in cui pensa la maggior parte dei fisici della materia condensata.
La curvatura di Berry determina effetti topologici nei sistemi fuori equilibrio perché quando viene applicato un campo elettrico un elettrone viene accelerato, quindi il suo slancio cambia. Quando ciò accade, la sua funzione d'onda cambia lentamente, allo stesso modo in cui la `freccia' viene ruotata nel trasporto parallelo, e come risultato di questa rotazione graduale si genera una corrente trasversale (Hall). Le relazioni Onsager, fondamentali per la fisica del non equilibrio, diciamo che la corrente di Hall non dissipa energia. Il caso estremo è l'effetto Hall anomalo quantistico (QAHE), un effetto quantistico chiave per la funzione dei materiali topologici, in cui le correnti di bordo possono fluire con una resistenza elettrica effettivamente nulla.
("Quantum" descrive la transizione "step" nella resistenza trasversale (Hall), cioè, varia in passaggi discreti piuttosto che in modo uniforme, mentre "anomalo" si riferisce al verificarsi del fenomeno in assenza di qualsiasi campo magnetico applicato.)
I ricercatori cercano di migliorare il QAHE per proteggere il comportamento topologico a temperature più elevate, consentendo l'elettronica topologica che sarebbe praticabile per il funzionamento a temperatura ambiente.
"La significativa riduzione della resistenza elettrica consentita dalla temperatura ambiente QAHE ci consentirebbe di ridurre significativamente il consumo di energia nei dispositivi elettronici, "dice Dimi.