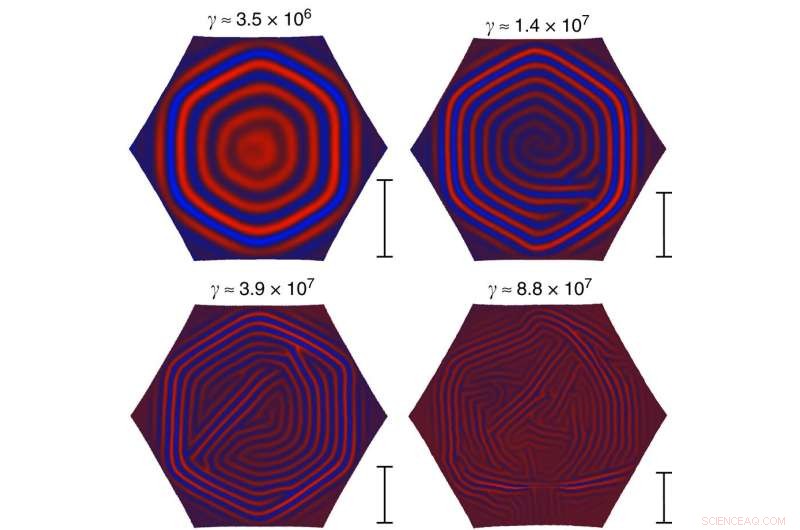
Ridimensionamento delle dimensioni del dominio. Tipici modelli di rughe di equilibrio in una sezione esagonale di un sottile guscio sferico su un substrato liquido. Tutti i parametri di simulazione vengono mantenuti fissi, ad eccezione dello spessore della lamiera. Il numero Föppl–von Kármán γ del sistema è indicato sopra ogni schema. Mentre il pattern in alto a sinistra è chiaramente diviso in sei domini, l'aumento di γ sembra diminuire la dimensione tipica del dominio. La barra della scala a destra di ciascun pattern mostra il ridimensionamento delle dimensioni tipiche del dominio previste dall'equazione (20), fino a un fattore costante (solo i rapporti tra le barre sono significativi poiché l'equazione (20) suggerisce solo il ridimensionamento della dimensione tipica e lascia il prefattore sconosciuto). Credito:Comunicazioni sulla natura (2017). DOI:10.1038/ncomms15809
Un oggetto che è intrinsecamente piatto, diciamo un pezzo di carta, può essere modellato in un cilindro senza allungarlo o strapparlo. Lo stesso non è vero, tuttavia, per qualcosa di intrinsecamente curvo come una lente a contatto. Quando vengono compressi tra due superfici piane o appoggiati sull'acqua, gli oggetti curvi si appiattiscono, ma con le rughe che si formano quando si piegano.
Ora, una ricerca dell'Università della Pennsylvania, dell'Università dell'Illinois Chicago (UIC) e della Syracuse University ha dimostrato che con alcune semplici geometrie è possibile prevedere i modelli di quelle rughe, sia dove si formeranno che in alcuni casi la loro direzione. I risultati, pubblicati su Nature Physics , hanno una serie di implicazioni, dal modo in cui i materiali interagiscono con l'umidità e riflettono la luce solare in natura al modo in cui un'elettronica flessibile potrebbe piegarsi.
"La bellezza di questo lavoro è quanto sia davvero semplice", afferma Eleni Katifori, professore associato presso il Dipartimento di Fisica e Astronomia della Penn. "Cosa c'è dietro è molto complicato, la fisica che si traduce in queste regole l'abbiamo trovata, ma le regole stesse sono molto semplici. È stimolante."
Incontro delle menti
Dal suo dottorato di ricerca lavoro, Katifori si è interessato alla meccanica della curvatura delle membrane sottili. Sebbene questa sia rimasta una curiosità, il suo percorso di ricerca ha virato invece verso le reti a flusso fluido. Poi, mentre collaborava a un progetto con il collega di Penn Randall Kamien e poi con il collega post-dottorato Hillel Aharoni, Katifori ha osservato qualcosa che non riusciva a spiegare in quel momento. "In altre parole, abbiamo notato la formazione di rughe nei domini", afferma.
In altre parole, quando una superficie curva si appiattisce, si ritrova con materiale in eccesso e conseguenti grinze. Quelle rughe emergono in modelli o settori. "La domanda è diventata, perché le rughe si dispongono in quel modo?" dice Katifori. "Non abbiamo capito quanto siano veramente importanti i domini nel wrinkling."
In una conferenza nel 2016, il matematico Ian Tobasco, assistente professore all'UIC, ha ascoltato Aharoni tenere un discorso sull'argomento. "Era la prima volta che vedevo presentare questo modello di sistema", afferma Tobasco. "Ho pensato che fosse davvero bello." A metà del 2017, Katifori, Aharoni e colleghi hanno pubblicato risultati sull'argomento in Nature Communications , poi in un seminario nello stesso anno, Tobasco incontrò Joseph Paulsen di Siracusa, che aveva presentato i dati preliminari sulla sperimentazione che il suo gruppo aveva fatto sulle rughe.
All'inizio del 2018, Tobasco ha iniziato a lavorare seriamente su una teoria matematica per le rughe e durante il pranzo in una conferenza quell'estate, Katifori, Tobasco e Paulsen hanno convenuto di condividere un interesse per questo problema. Hanno deciso di collaborare, concentrandosi sull'analisi di quanto la forma fisica del materiale e la curvatura da cui parte potrebbero essere importanti per i modelli di rughe.
Risolvere il problema
Per alcuni sfondi, la curvatura può essere positiva, come la rotondità di una palla da baseball o di un globo, o negativa, come la sella di un cavallo o il punto su una bottiglia di vetro dove il collo incontra la base. C'è anche del materiale piatto, come un pezzo di carta.
In questo lavoro, i ricercatori si sono concentrati sui gusci curvi positivamente e negativamente.
Da ciascuno hanno quindi rimosso le forme di base, come triangoli, quadrati e ovali. "Pensa a un tagliabiscotti. Diciamo che prendo un oggetto con una curvatura positiva o negativa, quindi ritaglia una di queste forme e la appoggio sul liquido", dice Katifori. Sarebbe possibile indovinare i modelli delle rughe e calcolare la direzione in cui scorrono le rughe? Per ogni forma, Tobasco risolveva la teoria sulla base dei principi fondamentali su cui aveva elaborato e pubblicato, quindi elaborava previsioni.
Sulla base di questi risultati, la ricercatrice post-dottorato di Katifori e Penn Desislava Todorova ha quindi condotto simulazioni, inserendo forme e parametri individuali in un programma per computer. Un lavoro simile stava accadendo nel laboratorio gestito da Paulsen, un assistente professore di fisica a Syracuse, attraverso esperimenti che stava eseguendo su pellicola di polistirene 1.000 volte più sottile di un pezzo di carta. "È realizzato con lo stesso materiale delle arachidi da imballaggio", afferma Tobasco, "ma invece della forma tridimensionale di un'arachide da imballaggio, immagina che sia piatto come un foglio".
Attraverso le simulazioni, la sperimentazione e molto avanti e indietro per perfezionare il processo ed espandere la teoria originale, il trio ha iniziato a discernere che applicando semplici principi geometrici, potevano sapere in anticipo quale modello avrebbero preso le rughe e per un sottoinsieme —quelle che descrivono come rughe "ordinate", in quale direzione correrebbero.
I principi geometrici
Per spiegare uno di questi principi, Katifori usa un poligono a cinque lati. "Prima inscrivo un cerchio nel poligono", dice. "I punti in cui quel cerchio tocca i bordi del poligono determinano dove disegno le mie linee." Si ferma per creare una seconda forma all'interno della prima, questa con quattro lati irregolari; inizia ogni linea dove si incontrano il cerchio e il poligono esterno, collegando tutte e quattro le linee interne. "Ora ho uno, due, tre, quattro, cinque domini", continua, indicando il quintetto delle sezioni appena transennate.
Per forme semplici come questa, le sezioni esterne conterranno rughe ordinate, organizzate e ordinate, seguendo la direzione delle linee interne disegnate da Katifori. All'interno del nuovo poligono interno, le rughe si formano ancora, ma rimangono disordinate e imprevedibili.
Tobasco indica un altro esempio, uno che ha determinato fosse universalmente vero per le forme tagliate da gusci curvati negativamente. "Alla fine, è molto semplice prevedere i modelli delle rughe. Tutto quello che devi fare è disegnare segmenti di linea che incontrino il confine ad angolo retto". In altre parole, inizia da un punto all'interno della forma e crea una linea diretta al bordo della forma, ma solo in un punto in cui si formerà un angolo retto.
Ci è voluto un anno perché la squadra capisse. "Le equazioni che determinano la disposizione delle rughe sono orrende da risolvere e molti dei modelli che abbiamo osservato nei nostri esperimenti e simulazioni sono piuttosto complicati", afferma Paulsen. "Ma si scopre che in un determinato insieme di condizioni, puoi prevedere il layout delle rughe con un semplice insieme di regole. Ciò significa che ora abbiamo un modo rapido ed efficiente per progettare modelli di rughe".
"La sua semplicità è bellissima ed è anche utile", aggiunge, in particolare per le superfici rugose che svolgono una funzione come consentire l'adesione o il flusso del fluido.
Katifori cita esempi simili. "Diciamo che c'è umidità o umidità nell'aria. L'acqua si comporterà in modo diverso nelle valli e sulle colline di una superficie scanalata", dice. "Controllando la formazione delle rughe, forse puoi influenzare il modo in cui l'acqua si condenserà."
Cosa verrà dopo
I ricercatori hanno ancora molto da capire su queste complesse superfici strutturate, come come estrarre modelli da rughe disordinate, perché domini ordinati e disordinati possono coesistere e perché c'è una "reciprocità" che collega gusci curvi negativamente e positivamente, il che significa che una volta il modello per uno è determinato, è semplice prevedere il modello per l'altro.
Per ora, tuttavia, si dicono entusiasti del potenziale di ciò che hanno imparato fino a questo punto.
"Hai una teoria complicata che, alla fine, si riduce a una matematica relativamente semplice che quasi chiunque può fare con un compasso e un righello", dice Katifori. "È una soluzione elegante e bella per un problema complesso." + Esplora ulteriormente