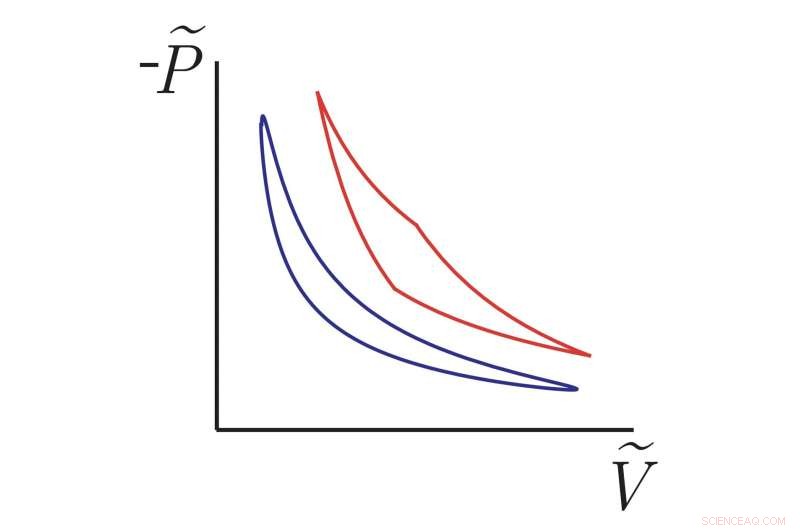
I cicli termodinamici recentemente scoperti (curva blu uniforme) si avvicinano a un nuovo limite geometrico sull'efficienza, superando altri motori di non equilibrio come il ciclo di Carnot (curva rossa) che opera a tempo finito. Gli assi verticale e orizzontale rappresentano gli analoghi della pressione (negativa) e del volume per un motore microscopico costituito da una particella attaccata a una molla che viene colpita dalle fluttuazioni termiche del suo ambiente. Queste sono curve teoriche basate sui nostri risultati matematici, ma gli sperimentatori hanno recentemente ideato metodi per misurare l'efficienza di questi tipi di sistemi in modo che i nostri risultati possano essere testati. Credito:Frim &DeWeese.
La termodinamica stocastica è un'area emergente della fisica volta a comprendere e interpretare meglio i concetti termodinamici lontano dall'equilibrio. Negli ultimi anni, le scoperte in questi campi hanno rivoluzionato la comprensione generale dei diversi processi termodinamici che operano in un tempo finito.
Adam Frim e Mike DeWeese, due ricercatori dell'Università della California, Berkeley (UC Berkeley), hanno recentemente condotto uno studio teorico esplorando l'intero spazio dei cicli termodinamici con una temperatura del bagno in continuo cambiamento. I loro risultati, presentati in un documento pubblicato in Physical Review Letters , sono stati ottenuti con metodi geometrici. La geometria termodinamica è un approccio alla comprensione della risposta dei sistemi termodinamici attraverso lo studio dello spazio geometrico di controllo.
"Ad esempio, per un gas in un pistone, una coordinata in questo spazio di controllo potrebbe corrispondere al volume controllato sperimentalmente del gas e un'altra alla temperatura", ha detto DeWeese a Phys.org. "Se uno sperimentatore dovesse girare quelle manopole, ciò traccia una traiettoria in questo spazio termodinamico. Ciò che fa la geometria termodinamica è assegnare a ciascuna curva una 'lunghezza termodinamica' corrispondente alla minima energia dissipata possibile di un dato percorso.'
La geometria termodinamica consente ai ricercatori di esaminare interessanti domande di ricerca, come il modo ottimale per manipolare un dato sistema nanoscopico, cancellare un po' di informazioni o costruire un motore termico classico o quantistico.
"Il nostro obiettivo principale in questo documento era capire il modo più efficiente per far funzionare un motore microscopico in modo che produca il lavoro più utile per la quantità di carburante che consuma", ha detto DeWeese a Phys.org. "Mentre la maggior parte dei precedenti studi di geometria termodinamica si concentrava sull'ottimizzazione del controllo di un sistema con determinate impostazioni iniziali e finali, eravamo interessati a costruire curve chiuse ottimali che potessero funzionare come motori termici altamente efficienti."
Le principali "regole" per capire come far funzionare in modo efficiente grandi motori, come quelli all'interno delle automobili, quando azionati lentamente, furono delineate per la prima volta oltre un secolo fa, quando furono formulate per la prima volta le leggi della termodinamica. Nel loro articolo, Frim e DeWeese hanno esteso queste teorie in modo che potessero essere applicate anche a motori microscopici che funzionano in un tempo finito. A differenza dei grandi motori a funzionamento lento, questi motori non sono in equilibrio termico con il mondo esterno e sono fortemente influenzati dalle fluttuazioni termiche dell'ambiente circostante.
"In qualsiasi corso universitario di termodinamica, apprendiamo che se si traccia la pressione rispetto al volume di un gas in una bombola e si considera qualsiasi ciclo chiuso che ritorna allo stesso punto del grafico, l'area contenuta all'interno della curva fornisce la quantità di utile lavoro che ottieni da un ciclo di questo motore termico", ha detto DeWeese. "Ciò presuppone che ti muovi molto lentamente lungo il ciclo, in modo che il gas nel cilindro rimanga sempre vicino all'equilibrio con il mondo esterno. C'è un'analogia con questo diagramma PV per motori microscopici, come una piccola particella attaccata a una molla essere colpito dalle fluttuazioni termiche del suo ambiente."
Quando hanno tracciato i cicli sull'analogo di un diagramma PV per un motore microscopico, Frim e DeWeese hanno scoperto che una funzione particolare dell'area contenuta all'interno della curva chiusa può ancora essere considerata come la quantità di lavoro utile fornito da un ciclo del motore . Inoltre, la lunghezza della curva chiusa è risultata correlata alla quantità di "lavoro utile" perso per dissipazione (cioè il riscaldamento dell'ambiente senza andare verso il funzionamento del motore).
"Il nostro risultato è concettualmente relativamente semplice", ha spiegato DeWeese. "Nella geometria termodinamica, la lunghezza è qualcosa di simile alla dissipazione. Quindi, abbiamo quindi pensato:se prendi un ciclo (un anello chiuso) con un perimetro che ha una lunghezza fissa, cosa rappresenta l'area all'interno di questo anello? va qualcosa come l'output di lavoro del ciclo, quindi in realtà i cicli ottimali dovrebbero avere una bassa dissipazione e un lavoro ad alto rendimento, cioè una piccola lunghezza e un'area ampia."
Sfruttando i risultati geometrici classici, i ricercatori sono stati quindi in grado di identificare protocolli ottimali che fissano un limite all'efficienza di tutti i cicli chiusi. Le loro scoperte potrebbero contribuire in modo significativo alla progettazione e allo sviluppo di efficienti motori termici microscopici. Il limite all'efficienza dei cicli termodinamici irreversibili stabilito da questo team di ricercatori è generale, quindi le sue implicazioni potrebbero andare ben oltre gli specifici motori microscopici considerati nel loro articolo.
"Uno dei nostri obiettivi a lungo termine è sviluppare la teoria necessaria agli ingegneri per progettare e costruire motori molto piccoli ed efficienti", ha affermato DeWeese. "Questa potrebbe rivelarsi un'area importante della nanotecnologia. Siamo anche fortemente motivati a comprendere la struttura e la funzione dei motori molecolari e di altri tipi di 'macchine' molecolari che vediamo nelle cellule di tutte le creature e piante."
Nel loro lavoro, De Weese e Frim ipotizzano che l'evoluzione naturale potrebbe aver scelto macchine molecolari efficienti. Se così fosse, le regole che hanno scoperto potrebbero essere un primo passo per poter prevedere la struttura e la funzione delle macchine molecolari che sono onnipresenti in biologia.
"Le disuguaglianze isoperimetriche (cioè l'interazione di lunghezze e aree di curve chiuse) negli approcci geometrici alla fisica potrebbero avere una miriade di implicazioni in futuro", ha aggiunto DeWeese. "Il nostro limite matematico è più realistico dei risultati precedenti che presupponevano che il motore fosse sempre molto vicino all'equilibrio termico con l'ambiente (o bagno di calore), ma assumiamo comunque che il sistema venga guidato lentamente (cioè i parametri di controllo sono cambiati lentamente). Ora siamo interessati ad estendere i nostri risultati oltre questo regime per includere sistemi più lontani dall'equilibrio". + Esplora ulteriormente
© 2022 Rete Science X