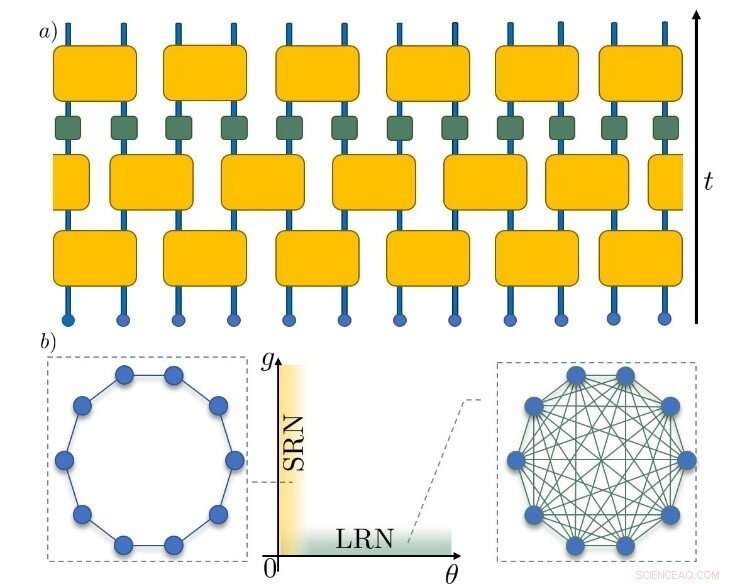
Figura 1. Rappresentazione schematica del modello Unitary Circuit Map. (a) La freccia nera a destra mostra la direzione del tempo mentre le particelle, rappresentate da piccoli cerchi blu, si evolvono. I quadrati gialli rappresentano le trasformazioni che accoppiano le particelle. I quadrati verdi indicano le trasformazioni non lineari che inducono il caos. (b) A seconda dei parametri selezionati, l'accoppiamento interparticellare può essere di natura a corto raggio (sinistra) oa lungo raggio (destra). Questo alla fine influenza le scale temporali emergenti delle dinamiche caotiche. Credito:Istituto per le scienze di base
Un esempio popolare di comportamento caotico è l'effetto farfalla:una farfalla può sbattere le ali da qualche parte nell'Oceano Atlantico e causare un tornado in Colorado. Questa straordinaria favola illustra come l'estrema sensibilità della dinamica dei sistemi caotici possa produrre risultati drammaticamente diversi nonostante lievi differenze nelle condizioni iniziali. Le leggi fondamentali della natura che governano la dinamica dei sistemi fisici sono intrinsecamente non lineari, portando spesso al caos e alla successiva termalizzazione.
Tuttavia ci si potrebbe chiedere perché non c'è un aumento dilagante dei tornado in Colorado causato da una massiccia delusione delle farfalle negli affari globali, come ad esempio il riscaldamento globale? Questo perché le dinamiche fisiche, sebbene caotiche, sono in grado di dimostrare stati notevolmente stabili. Un esempio è la stabilità del nostro sistema solare:obbedisce alle leggi della fisica non lineari, che possono apparentemente indurre il caos nel sistema.
La ragione di questa stabilità si basa sul fatto che i sistemi debolmente caotici possono mostrare dinamiche periodiche molto ordinate che possono durare per milioni di anni. Questa scoperta fu fatta negli anni '50 dai grandi matematici Kolmogorov, Arnold e Moser. La loro scoperta, tuttavia, funziona solo nel caso di sistemi con un numero ridotto di elementi interagenti. Se il sistema include molte parti costitutive, allora il suo destino non è ben compreso.
I ricercatori del Center for Theoretical Physics of Complex Systems (PCS) all'interno dell'Institute for Basic Science (IBS), in Corea del Sud, hanno recentemente introdotto un nuovo framework per caratterizzare dinamiche debolmente caotiche in sistemi complessi contenenti un gran numero di particelle costituenti. Per raggiungere questo obiettivo, hanno utilizzato un modello basato sull'informatica quantistica, la mappa dei circuiti unitari, per simulare il caos.
Indagare le scale temporali della caoticità è un compito impegnativo, che richiede metodi computazionali efficienti. Il modello Unitary Circuit Map implementato in questo studio risponde a questo requisito. "Il modello consente una propagazione degli stati nel tempo efficiente e senza errori", spiega Merab Malishava, "che è essenziale per modellare una caoticità estremamente debole in sistemi di grandi dimensioni. Tali modelli sono stati utilizzati per ottenere tempi di evoluzione non lineare da record prima, che era fatto anche nel nostro gruppo."
Di conseguenza, sono stati in grado di classificare le dinamiche all'interno del sistema identificando scale di tempo e lunghezza che emergono quando la termalizzazione rallenta drasticamente. I ricercatori hanno scoperto che se le parti costituenti sono collegate in una rete a lungo raggio (LRN) (ad esempio in modo tutto-tutto), le dinamiche di termalizzazione sono caratterizzate da un'unica scala temporale, chiamata tempo di Lyapunov. Tuttavia, se l'accoppiamento è di natura di rete a corto raggio (SRN) (ad esempio il vicino più vicino), emerge un'ulteriore scala di lunghezza correlata al congelamento di parti più grandi del sistema per lunghi periodi con rari schizzi caotici.
Tipicamente gli studi su tali dinamiche sensibili vengono effettuati utilizzando le tecniche di analisi del comportamento degli osservabili. Queste tecniche risalgono agli anni '50 quando furono effettuati i primi esperimenti sulla caoticità e termalizzazione. Gli autori hanno identificato un nuovo metodo di analisi, studiando il ridimensionamento dello spettro di Lyapunov.
Merab Malishava afferma:"I metodi precedenti potrebbero portare a risultati ambigui. Scegli un osservabile e apparentemente noti la termalizzazione e pensi che la dinamica sia caotica. Tuttavia, se si studia un altro osservabile, da un'altra prospettiva, si conclude che il sistema è congelato e niente cambia, senza terminizzazione. Questa è l'ambiguità, che abbiamo superato. Lo spettro di Lyapunov è un insieme di scale temporali che caratterizzano la dinamica in modo completo e completo. E per di più, è la stessa da ogni punto di vista! Unico e inequivocabile."
I risultati non sono solo interessanti da un punto di vista fondamentale. Hanno anche il potenziale per far luce sulle realizzazioni dei computer quantistici. Il calcolo quantistico richiede una dinamica coerente, il che significa nessuna termalizzazione. Nel lavoro in corso, è stato studiato un drammatico rallentamento della dinamica termica con quantità emergenti quasi conservate. Quantizzare questo caso potrebbe forse spiegare fenomeni come la localizzazione di molti corpi, che è una delle idee di base per evitare la termalizzazione nei computer quantistici.
Un altro grande risultato dello studio riguarda l'applicabilità dei risultati alla stragrande maggioranza dei modelli fisici che vanno dalle semplici reti di oscillatori alle complesse dinamiche delle reti di spin. Il Dr. Sergej Flach, leader del gruppo di ricerca e direttore di PCS spiega:"Abbiamo lavorato per cinque anni allo sviluppo di un framework per classificare le dinamiche debolmente caotiche nei sistemi macroscopici, che ha portato a una serie di lavori che hanno fatto avanzare significativamente l'area . Abbiamo messo da parte studi caso per caso strettamente focalizzati a favore della promozione di un approccio concettuale che sia affidabile e riconoscibile in un gran numero di realizzazioni fisiche. Questo lavoro specifico è un elemento costitutivo molto importante nel quadro di cui sopra. Abbiamo scoperto che un il modo tradizionale di vedere le cose a volte non è il più informativo e offre un nuovo approccio alternativo. Il nostro lavoro non si ferma affatto qui, poiché non vediamo l'ora di far avanzare la scienza con idee più rivoluzionarie."
Questa ricerca è stata recentemente pubblicata in Physical Review Letters. + Esplora ulteriormente