In una nuova pubblicazione in Physical Review Letters , i ricercatori di Amsterdam dimostrano un modo per descrivere i sistemi di spin-bosoni e utilizzarli per configurare in modo efficiente i dispositivi quantistici in uno stato desiderato.

I dispositivi quantistici sfruttano il comportamento bizzarro delle particelle quantistiche per eseguire compiti che vanno oltre ciò che possono fare le macchine “classiche”, tra cui il calcolo quantistico, la simulazione, il rilevamento, la comunicazione e la metrologia. Questi dispositivi possono assumere molte forme, come un insieme di circuiti superconduttori o un reticolo di atomi o ioni tenuti in posizione da laser o campi elettrici.

Indipendentemente dalla loro realizzazione fisica, i dispositivi quantistici sono generalmente descritti in termini semplificati come una raccolta di bit o spin quantistici a due livelli interagenti. Tuttavia, questi spin interagiscono anche con altre cose nell’ambiente circostante, come la luce nei circuiti superconduttori o le oscillazioni nel reticolo di atomi o ioni. Particelle di luce (fotoni) e modi vibrazionali di un reticolo (fononi) sono esempi di bosoni.

A differenza degli spin, che hanno solo due possibili livelli di energia ("0" o "1"), il numero di livelli per ciascun bosone è infinito. Di conseguenza, ci sono pochissimi strumenti computazionali per descrivere gli spin accoppiati ai bosoni.

Nel loro nuovo lavoro, i fisici Liam Bond, Arghavan Safavi-Naini e Jiří Minář dell'Università di Amsterdam, QuSoft e Centrum Wiskunde &Informatica aggirano questa limitazione descrivendo sistemi composti da spin e bosoni utilizzando i cosiddetti stati non gaussiani. Ogni stato non gaussiano è una combinazione (una sovrapposizione) di stati gaussiani molto più semplici.

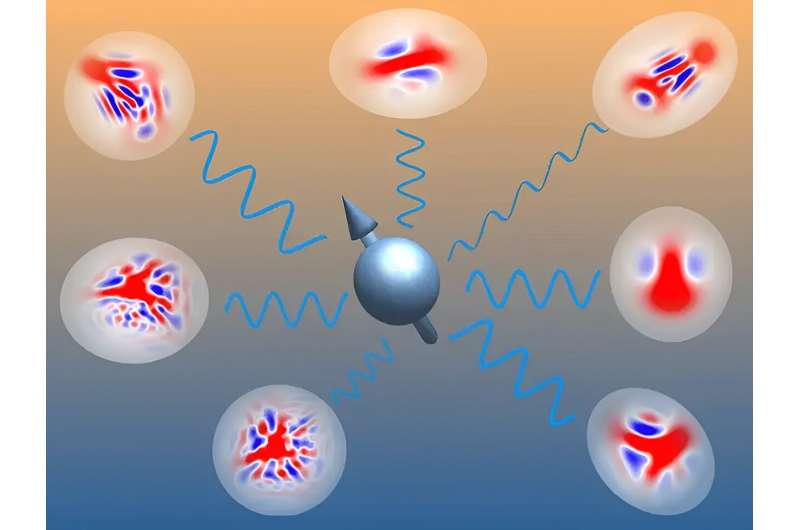
Ogni modello blu-rosso nell'immagine sopra rappresenta un possibile stato quantistico del sistema spin-bosone. "Uno stato gaussiano apparirebbe come un semplice cerchio rosso, senza interessanti schemi blu-rossi", spiega Ph.D. il candidato Liam Bond. Un esempio di stato gaussiano è la luce laser, in cui tutte le onde luminose sono perfettamente sincronizzate.

"Se prendiamo molti di questi stati gaussiani e iniziamo a sovrapporli (in modo che siano in sovrapposizione), emergono questi modelli meravigliosamente intricati. Eravamo particolarmente entusiasti perché questi stati non gaussiani ci permettono di conservare molte delle potenti conoscenze matematiche meccanismo esistente per gli stati gaussiani, consentendoci al tempo stesso di descrivere un insieme molto più diversificato di stati quantistici," afferma Bond.

"Ci sono così tanti modelli possibili che i computer classici spesso faticano a calcolarli ed elaborarli. Invece, in questa pubblicazione utilizziamo un metodo che identifica il più importante di questi modelli e ignora gli altri. Questo ci permette di studiare questi sistemi quantistici e di progettare nuovi modi per preparare interessanti stati quantistici."

Il nuovo approccio può essere sfruttato per preparare in modo efficiente gli stati quantistici in un modo che supera gli altri protocolli utilizzati tradizionalmente. "La preparazione rapida dello stato quantistico potrebbe essere utile per un'ampia gamma di applicazioni, come la simulazione quantistica o anche la correzione degli errori quantistici", osserva Bond.

I ricercatori dimostrano anche di poter utilizzare stati non gaussiani per preparare stati quantistici "critici" che corrispondono a un sistema sottoposto a una transizione di fase. Oltre all'interesse fondamentale, tali stati possono migliorare notevolmente la sensibilità dei sensori quantistici.

Sebbene questi risultati siano molto incoraggianti, rappresentano solo un primo passo verso obiettivi più ambiziosi. Finora il metodo è stato dimostrato per un singolo giro. Un'estensione naturale, ma impegnativa, è quella di includere molti spin e molti modi bosonici allo stesso tempo. Una direzione parallela è quella di tenere conto degli effetti dell’ambiente che disturba i sistemi spin-bosone. Entrambi questi approcci sono in fase di sviluppo attivo.