Aggiungere una semplice regola a un gioco di biliardo idealizzato porta a una ricchezza di intriganti domande matematiche, nonché ad applicazioni nella fisica degli organismi viventi. Questa settimana, i ricercatori dell'Università di Amsterdam, tra cui due studenti di master come primi autori, hanno pubblicato un articolo su Physical Review Letters sulle affascinanti dinamiche del biliardo con memoria.
Una versione idealizzata del gioco del biliardo affascina i matematici da decenni. La domanda fondamentale è semplice:una volta giocata una palla da biliardo, dove va e dove finisce? Supponiamo che il biliardo sia perfetto:le pareti rimbalzano perfettamente, non ci sono altri oggetti sul tavolo, il movimento della palla è privo di attrito e così via. Allora la palla non "finirà" realmente da nessuna parte; andrà avanti per sempre.
Ma ritorna mai al punto di partenza? Alla fine visita ogni parte del tavolo? Quando cambiamo leggermente la direzione della palla, o la sua posizione di partenza, il percorso che segue assomiglia a quello precedente?
Tutte queste domande risultano molto intriganti da un punto di vista matematico. Le loro risposte non sono sempre note, soprattutto quando la forma del biliardo non è semplice, come un quadrato o un rettangolo. Ad esempio, nei biliardi triangolari con angoli inferiori a 100 gradi, è noto che esistono sempre percorsi periodici, percorsi che la pallina può seguire e che ritornano su se stessi.
Ciò può essere dimostrato matematicamente. Ora, cambia uno degli angoli con un angolo leggermente più grande e nessun matematico saprà più la risposta.
I giochi di biliardo idealizzati non sono solo il passatempo preferito dei matematici. Hanno anche un profondo impatto sulla fisica e sulle altre scienze. Molte delle domande sul biliardo possono essere formulate come domande sul caos:condizioni iniziali simili di un sistema dinamico (che si tratti di una palla su un tavolo da biliardo, di una molecola in un gas o di un uccello in uno stormo) portano sempre a risultati finali simili. risultati?
In una ricerca condotta presso l'Università di Amsterdam, un team di fisici si è accorto che modificando leggermente le regole del gioco del biliardo, il numero di applicazioni nel mondo reale aumenta ulteriormente.
Mazi Jalaal, coautore della pubblicazione e capo del gruppo in cui è stata condotta la ricerca, spiega:"In natura, molti organismi viventi hanno una forma esterna di memoria. Ad esempio, lasciano tracce per ricordare dove sono stati. Possono quindi utilizzare tali informazioni per seguire di nuovo lo stesso percorso o, ad esempio, durante la ricerca di cibo, per non esplorare di nuovo la stessa regione."
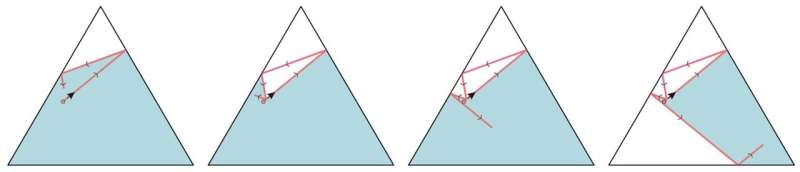
Quest’ultima opzione ha portato i ricercatori a un’idea interessante:cosa succederebbe se aggiungessimo una regola al gioco del biliardo, cioè che la palla non possa mai incrociare il suo percorso precedente? Il risultato è che la dimensione effettiva del tavolo da biliardo diventa sempre più piccola. Infatti, la palla alla fine rimane intrappolata nella sua stessa traiettoria.
Nuove domande intriganti
L'effetto intrappolamento rende il sistema ancora più intrigante. Anche le domande più semplici ora diventano estremamente affascinanti. Quanta distanza percorre una palla prima di rimanere intrappolata? La risposta varia, sia dalla forma del tavolo che dal punto di partenza e direzione della pallina.
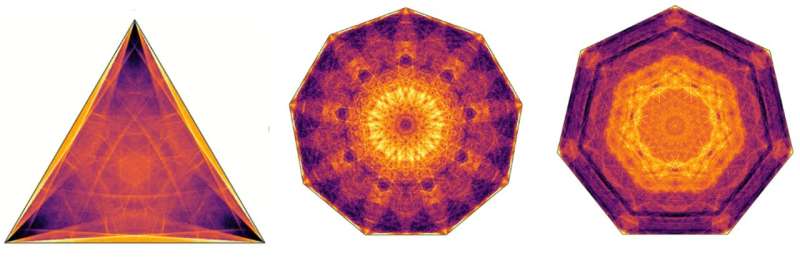
A volte la pallina percorre una lunghezza che è solo poche volte la dimensione del tavolo, a volte può percorrere 100 volte quella lunghezza prima di rimanere intrappolata. Anche dove la palla alla fine finisce nel suo stato intrappolato è una questione complessa; ripetere l'esperimento su un computer milioni di volte, ogni volta con una posizione iniziale e una velocità leggermente diverse, porta a bellissimi modelli di configurazioni finali.
L'immagine all'inizio di questo testo mostra alcuni di questi bellissimi esempi. È interessante notare che i sistemi dinamici risultanti possono essere caotici. Cambiare solo leggermente la posizione iniziale o la velocità della palla che evita se stessa può farla rimanere intrappolata in un punto completamente diverso del biliardo.
Inoltre, contrariamente a quanto accade su un normale tavolo da biliardo, la palla che si evita non ha la stessa probabilità di finire ovunque. Alcune regioni sono più probabili di altre. Per spiegare e dimostrare tutte queste caratteristiche, i matematici hanno sicuramente il loro bel da fare.
Una particolarità interessante della pubblicazione è che entrambi i suoi primi autori sono studenti magistrali. Jalaal aggiunge:"L'idea di un 'biliardo con memoria' è abbastanza semplice e nuova che studiarla non richiede anni di esperienza. Thijs e Stijn hanno fatto un ottimo lavoro nel rendere proprio il materiale e nel trovare modi intelligenti per studiare tutti questi nuovi problemi aperti. Sono molto felice che possano già essere autori principali di una pubblicazione."
I risultati sono solo i primi passi in quella che potrebbe essere un’area di ricerca completamente nuova. Non solo ci sono molte domande matematiche interessanti che ora attendono una risposta; infinite sono anche le applicazioni in fisica, compresa la biofisica.
Jalaal afferma:"Il concetto di intrappolamento richiede di essere esplorato, anche nei sistemi della vita reale. Ad esempio, sappiamo che le muffe melmose unicellulari utilizzano percorsi di autoevitamento. Anche loro rimangono intrappolate e cosa succede quando lo fanno? Oppure dispongono di meccanismi intelligenti per evitare che ciò accada? Lo usano per migliorare le strategie di ricerca del cibo?
"I risultati ci aiuterebbero a comprendere meglio questi sistemi biologici e forse anche a incorporare le lezioni che impariamo per ottimizzare questa forma di biliardo con memoria per l'uso nei robot."
Ulteriori informazioni: Thijs Albers et al, Biliardo con memoria spaziale, Lettere di revisione fisica (2024). DOI:10.1103/PhysRevLett.132.157101. Su arXiv :DOI:10.48550/arxiv.2307.01734
Informazioni sul giornale: Lettere di revisione fisica , arXiv
Fornito dall'Università di Amsterdam