Nel campo della fisica, le dimensioni sintetiche (SD) sono emerse come una delle frontiere della ricerca attiva, offrendo un percorso per esplorare fenomeni in spazi dimensionali superiori, oltre il nostro spazio geometrico 3D convenzionale. Il concetto ha raccolto un'attenzione significativa, soprattutto nella fotonica topologica, grazie al suo potenziale di sbloccare una fisica ricca inaccessibile nelle dimensioni tradizionali.
I ricercatori hanno proposto vari quadri teorici per studiare e implementare le DS, con l'obiettivo di sfruttare fenomeni come campi di Gauge sintetici, fisica quantistica di Hall, solitoni discreti e transizioni di fase topologiche in quattro dimensioni o superiori. Tali proposte potrebbero portare a nuove comprensioni fondamentali in fisica.
Una delle sfide principali nello spazio 3D convenzionale è la realizzazione sperimentale di strutture reticolari complesse con accoppiamenti specifici. Gli SD offrono una soluzione, fornendo una piattaforma più accessibile per la creazione di reti complesse di risonatori con accoppiamenti anisotropi, a lungo raggio o dissipativi. Questa capacità ha già portato a dimostrazioni rivoluzionarie dell'avvolgimento topologico non hermitiano, della simmetria del tempo di parità e di altri fenomeni.
Una varietà di parametri o gradi di libertà all'interno di un sistema, come modalità di frequenza, modalità spaziali e momenti angolari orbitali, possono essere utilizzati per costruire SD, promettendo applicazioni in diversi campi che vanno dalle comunicazioni ottiche ai laser isolanti topologici.
Un obiettivo chiave in questo campo è la costruzione di una rete "utopica" di risonatori in cui qualsiasi coppia di modi possa essere accoppiata in modo controllato. Il raggiungimento di questo obiettivo richiede una manipolazione precisa della modalità all'interno dei sistemi fotonici, offrendo strade per migliorare la trasmissione dei dati, l'efficienza della raccolta di energia e la radianza della serie laser.

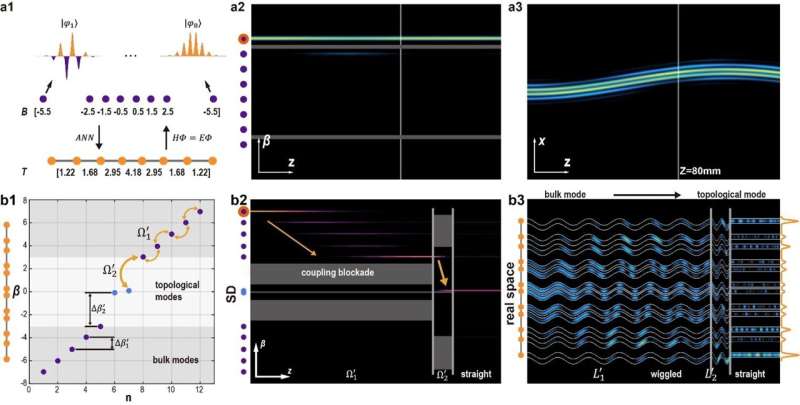
Ora, come riportato in Advanced Photonics , un team internazionale di ricercatori ha creato matrici personalizzabili di guide d'onda per stabilire dimensioni modali sintetiche. Questo progresso consente un controllo efficace della luce in un sistema fotonico, senza la necessità di complicate funzionalità extra come la non linearità o la non ermiticità.
Il professor Zhigang Chen dell'Università di Nankai osserva:"La capacità di regolare diverse modalità di luce all'interno del sistema ci porta un passo avanti verso il raggiungimento di reti 'utopistiche', dove tutti i parametri di un esperimento sono perfettamente controllabili."
Nel loro lavoro, i ricercatori modulano le perturbazioni (“frequenze oscillanti”) per propagazioni che corrispondono alle differenze tra le diverse modalità di luce. Per fare ciò, utilizzano reti neurali artificiali (ANN) per progettare array di guide d’onda nello spazio reale. Le ANN sono addestrate per creare configurazioni di guide d'onda che hanno esattamente i modelli di modalità desiderati. Questi test aiutano a rivelare come la luce si propaga e viene confinata all'interno degli array.
Infine, i ricercatori dimostrano l’uso delle ANN per progettare un tipo speciale di struttura reticolare fotonica chiamata reticolo Su-Schrieffer-Heeger (SSH). Questo reticolo ha una caratteristica specifica che consente il controllo topologico della luce in tutto il sistema. Ciò consente loro di modificare la modalità di massa in cui viaggia la luce, mostrando le proprietà uniche delle loro dimensioni sintetiche.
Le implicazioni di questo lavoro sono sostanziali. Mettendo a punto le distanze e le frequenze delle guide d'onda, i ricercatori mirano a ottimizzare la progettazione e la fabbricazione di dispositivi fotonici integrati.
Il professor Hrvoje Buljan dell'Università di Zagabria afferma:"Oltre alla fotonica, questo lavoro offre uno sguardo sulla fisica geometricamente inaccessibile. È promettente per applicazioni che vanno dal mode laser all'ottica quantistica e alla trasmissione dei dati."
Sia Chen che Buljan notano che l'interazione tra fotonica topologica e fotonica di dimensione sintetica potenziata dalle ANN apre nuove possibilità di scoperte che potrebbero portare a materiali e applicazioni di dispositivi senza precedenti.
Ulteriori informazioni: Shiqi Xia et al, Dinamiche delle dimensioni sintetiche potenziate dal deep learning:trasformazione della luce in modalità topologiche, Fotonica avanzata (2024). DOI:10.1117/1.AP.6.2.026005
Fornito da SPIE