Un piccolo team di fisici e ingegneri meccanici dell'Universidad de Antofagasta, dell'Universidad Autónoma de Chile e dell'Universidad de O'Higgins, tutte in Cile, ha trovato un modo per trovare i punti di stabilità di monostrati disposti granularmente in un unico mucchio con pendii inclinati. /P>

Nel loro studio, pubblicato sulla rivista Physical Review E , il gruppo ha utilizzato simulazioni al computer per modellare sfere, come le arance, impilate con bordi inclinati variabili per scoprire il punto in cui la pila collasserà quando una o più sfere vengono rimosse da un bordo.

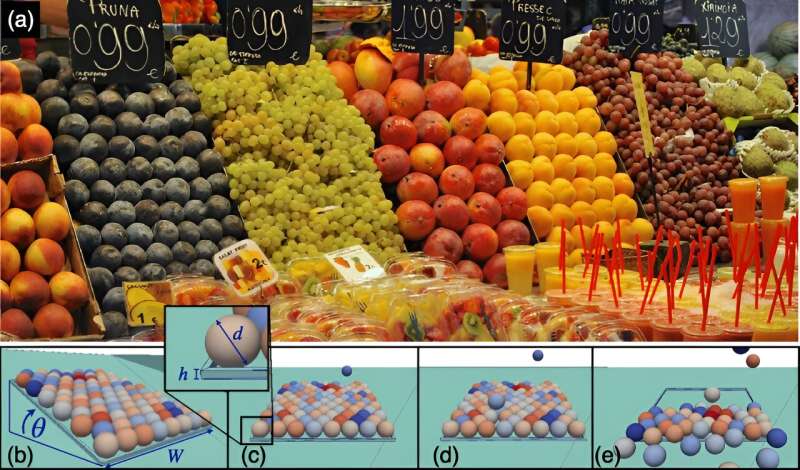
Molti negozi di alimentari espongono la frutta in vendita assemblando pile volte a metterne in mostra la bontà. Tali pile tendono ad avere bordi inclinati, dando un'immagine generale di instabilità:gli acquirenti incauti che prendono una singola arancia dalla parte sbagliata della pila possono provocare un crollo con la frutta che rotola dallo scaffale e sul pavimento. In questo nuovo sforzo, il gruppo di ricerca ha trovato i punti critici di tali pile.

I ricercatori hanno creato simulazioni raffiguranti sfere di varie dimensioni impilate con diverse pendenze dei bordi e le hanno eseguite in molteplici configurazioni, da pendenze modeste a estreme. Hanno scoperto che le sfere impilate con pendenze estreme possono effettivamente collassare se solo una singola sfera viene rimossa dal bordo inclinato. Hanno anche scoperto che, per pendenze modeste, è possibile rimuovere quasi un numero qualsiasi di sfere senza causare un collasso. È stato nel mezzo di tali estremi che le cose sono diventate più difficili da prevedere.

Aumentando lentamente l’angolo di inclinazione, hanno scoperto, si sono verificate situazioni in cui la rimozione di più sfere anziché di una sola potrebbe provocare il collasso. Hanno anche calcolato che in circostanze medie, come quelle tipiche di un negozio di alimentari, fino al 10% delle sfere (mele, arance o pompelmi, per esempio) devono essere rimosse prima di un crollo. Pertanto, è improbabile che un singolo acquirente provochi un collasso se rimuove anche un solo frutto, a meno che diversi acquirenti prima di loro non abbiano fatto lo stesso dalla stessa posizione.

I ricercatori intendono continuare il loro lavoro, esaminando altri possibili scenari di collasso nel mondo reale, come cumuli di rocce di diverse dimensioni.

Ulteriori informazioni: Eduardo Rojas et al, Stabilità di un monostrato granulare inclinato:quante sfere possiamo scegliere prima del collasso?, Revisione fisica E (2023). DOI:10.1103/PhysRevE.108.064904. Su arXiv :DOI:10.48550/arxiv.2206.03016

Informazioni sul giornale: Revisione fisica E , arXiv

© 2024 Rete Scienza X