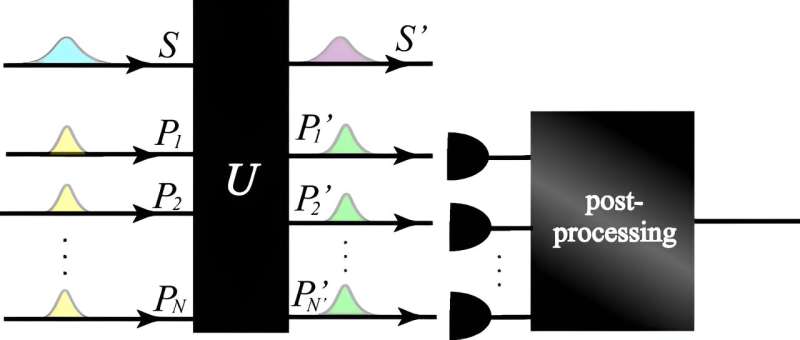
Uno studio pubblicato sulla rivista Physical Review Letters da ricercatori giapponesi risolve un problema di vecchia data della fisica quantistica ridefinendo il principio di indeterminazione.

Il principio di indeterminazione di Werner Heisenberg è una caratteristica chiave e sorprendente della meccanica quantistica, e per questo può ringraziare la sua febbre da fieno. Infelice a Berlino nell'estate del 1925, il giovane fisico tedesco andò in vacanza sulla remota e rocciosa isola di Helgoland, nel Mare del Nord, al largo della costa settentrionale della Germania. Le sue allergie migliorarono e poté continuare il suo lavoro cercando di comprendere le complessità del modello dell'atomo di Bohr, sviluppando tabelle di proprietà atomiche interne, come energia, posizione e quantità di moto.

Quando tornò a Gottinga, il suo consigliere, Max Born, riconobbe che ciascuna di queste tabelle poteva essere formata in una matrice, essenzialmente una tabella di valori bidimensionale. Insieme al 22enne Pasqual Jordan, hanno perfezionato il loro lavoro sulla meccanica delle matrici, la prima teoria di successo della meccanica quantistica, le leggi fisiche che descrivono piccoli oggetti come atomi ed elettroni.

Anche se nel giro di anni la meccanica delle matrici sarebbe stata sostituita dalla funzione d'onda di Schrödinger e dalla sua equazione, ciò permise a Heisenberg l'intuizione di formulare il principio di indeterminazione:esiste un limite a quanto precisamente la posizione e la quantità di moto di un sistema quantistico, tipicamente una particella, possono essere misurato.

Il limite del prodotto delle incertezze di misura delle due grandezze è h/4π, dove h è la costante di Planck, estremamente piccola ma comunque non nulla. In breve, non è possibile misurare sia la posizione che la quantità di moto di un oggetto quantistico con precisione arbitraria:misurarne uno con una precisione maggiore significa che l'altro può essere misurato solo con una precisione inferiore.

Da un punto di vista fisico, supponiamo di voler misurare la posizione e la quantità di moto di un elettrone. È necessario illuminare un sistema con una luce di qualche tipo per misurarne le proprietà. La luce è quantizzata come fotoni, che hanno un'energia diversa da zero. Far brillare un fotone sull'elettrone disturba necessariamente l'elettrone dal suo stato originale. Nella meccanica quantistica il semplice atto della misurazione impone un limite alla precisione della misurazione.

Incertezze simili valgono per le misurazioni del tempo e dell'energia, della posizione angolare e del momento angolare, e in generale di due variabili qualsiasi che non "commutano" se rappresentate come operatori nella rigorosa meccanica quantistica.

Alcuni decenni dopo il principio di indeterminazione fu perfezionato dai fisici Eugene Wigner, poi Huzihiro Araki e Mutsuo M. Yanase nel teorema Wigner-Araki-Yanase (WAY), che afferma che per due quantità osservabili q e p, dove p è conservato ( come la quantità di moto di un sistema), allora anche se p non viene misurato affatto, q non può essere misurato con precisione arbitraria.

"Come conseguenza del teorema WAY possiamo vedere che (in un certo senso) è impossibile misurare la posizione q della particella; tutto quello che possiamo misurare è la sua posizione relativa all'apparato, q—Q," dice il matematico John Baez Ha scritto l'Università della California, Riverside, dove Q è la posizione dell'apparecchio di misurazione.

Ma il teorema WAY si applica solo a quantità come la rotazione di una particella, che può richiedere solo quantità discrete e limitate.

Ora Yui Kuramochi dell’Università di Kyushu e Hiroyasu Tajima dell’Università di Elettro-Comunicazioni in Giappone hanno risolto un problema di lunga data dimostrando che il teorema WAY si applica anche a quantità osservabili che sono continue (non discrete) o illimitate, come la posizione.

"Secondo il principio di indeterminazione, la posizione e la quantità di moto non possono essere misurate con precisione simultaneamente", ha affermato Kuramochi. "Il nostro risultato impone un'ulteriore restrizione:anche solo la posizione stessa non può essere misurata con precisione, finché utilizziamo misurazioni naturali che soddisfino la conservazione della quantità di moto." La loro dimostrazione esamina un "operatore illimitato", quantità fisiche che possono assumere valori infinitamente grandi.

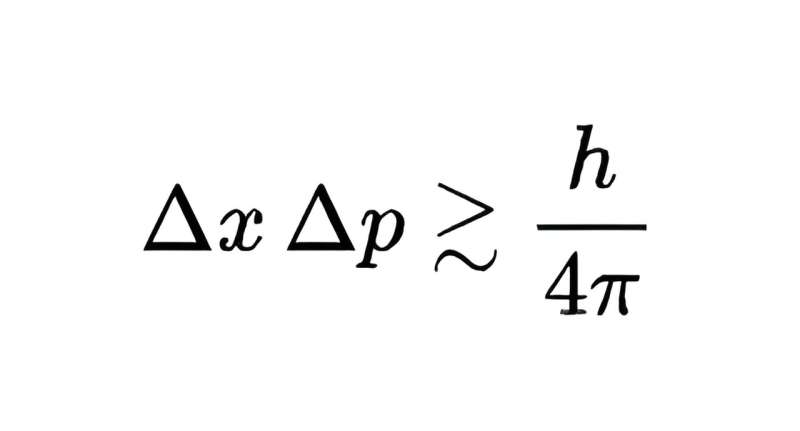
A rigor di termini, il risultato richiede una condizione particolare che è alla base del teorema WAY, chiamata condizione di Yanase. Pur essendo molto tecnico, stabilisce essenzialmente la compatibilità della variabile illimitata dell'apparato con la quantità conservata. La condizione Yanase, sebbene matematica, sembra auspicabile per le applicazioni ai sistemi fisici del mondo reale.

"Il teorema WAY prevede che secondo una legge di conservazione, una quantità fisica che non commuta con la carica conservata non può essere misurata senza errori", continua Kuramochi. "Ciò corrisponde a una risposta a un problema aperto da 60 anni. Il nuovo risultato risolve un problema vecchio di decenni su come affrontare tali osservabili continui e illimitati, specialmente in campi come l'ottica quantistica, dove è probabile che la nuova estensione del teorema trovi applicazioni ."

Il teorema originale di WAY proibisce che l'errore di misurazione sia zero, ma è un teorema qualitativo e non specifica il limite di misurazione e nemmeno se esiste un limite inferiore maggiore di zero. Lo stesso vale per questa estensione del teorema WAY di Kuramochi e Tajima.

Nel loro articolo gli autori scrivono che è ancora una questione aperta se il teorema originale di WAY per misurazioni ripetute possa essere generalizzato come hanno fatto, a osservabili conservati illimitati.

Suggerendo nuove direzioni di indagine sulle estensioni del teorema WAY, il team vorrebbe generalizzare i risultati agli stati con vincoli energetici, poiché i risultati attuali sono limitati a casi indipendenti dallo stato e a casi approssimati. Una potenziale applicazione è stabilire limiti su come i protocolli di trasmissione di rete quantistica possono funzionare meglio dei limiti classici.

Ulteriori informazioni: Yui Kuramochi et al, Teorema di Wigner-Araki-Yanase per osservabili conservati continui e illimitati, Lettere di revisione fisica (2023). DOI:10.1103/PhysRevLett.131.210201

Informazioni sul giornale: Lettere di revisione fisica

© 2023 Rete Scienza X