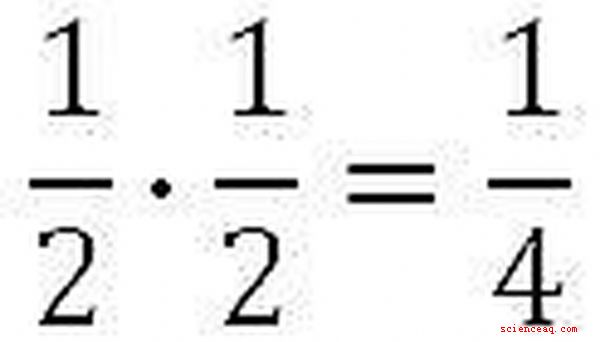
Questo è l'articolo 1 di una serie di articoli indipendenti sulla probabilità di base. Un argomento comune nella probabilità introduttiva è la risoluzione di problemi che coinvolgono coin flip. Questo articolo mostra i passaggi per risolvere i più comuni tipi di domande di base su questo argomento.

In primo luogo, si noti che il problema probabilmente farà riferimento a una moneta "giusta". Tutto ciò significa che non abbiamo a che fare con una moneta da "trucco", come quella che è stata ponderata per atterrare su un certo lato più spesso di quanto avrebbe fatto.

In secondo luogo, problemi come questo mai coinvolgere qualsiasi tipo di sciocchezza, come la moneta che atterra sul suo bordo. A volte gli studenti cercano di fare pressioni per avere una domanda ritenuta nulla e non valida a causa di uno scenario inverosimile. Non portare nulla nell'equazione come la resistenza al vento, o se la testa di Lincoln pesa più della sua coda, o qualsiasi cosa del genere. Abbiamo a che fare con 50/50 qui. Gli insegnanti si arrabbiano davvero per parlare di qualcos'altro.

Con tutto ciò che è stato detto, ecco una domanda molto comune: "Una moneta equa atterra sulla testa cinque volte di fila. Quali sono le probabilità che atterrerà testa al prossimo lancio? " La risposta alla domanda è semplicemente 1/2 o 50% o 0,5. È così. Qualsiasi altra risposta è sbagliata.

Smetti di pensare a qualunque cosa tu stia pensando in questo momento. Ogni lancio di una moneta è totalmente indipendente. La moneta non ha memoria. La moneta non si "annoia" di un dato risultato, e desidera passare a qualcos'altro, né ha alcun desiderio di continuare un particolare risultato poiché è "on a roll". Per essere sicuro, più volte si lancia una moneta, più si avvicina il 50% dei lanci alla testa, ma ciò non ha ancora nulla a che vedere con un singolo lancio. Queste idee comprendono ciò che è noto come l'errore del giocatore d'azzardo. Vedi la sezione Risorse per ulteriori informazioni.

Ecco un'altra domanda comune: "Una moneta buona viene girata due volte. Quali sono le probabilità che atterrerà sulla testa di entrambe le lanci?" Ciò di cui abbiamo a che fare qui sono due eventi indipendenti, con una condizione "e". Detto più semplicemente, ogni lancio della moneta non ha nulla a che fare con nessun altro lancio. Inoltre, abbiamo a che fare con una situazione in cui abbiamo bisogno di una cosa per accadere "e" un'altra cosa.

In situazioni come quella sopra, moltiplichiamo le due probabilità indipendenti insieme. In questo contesto, la parola "e" si traduce in moltiplicazione. Ogni flip ha una 1/2 possibilità di atterrare sulle teste, quindi moltiplichiamo 1/2 1/2 per ottenere 1/4. Ciò significa che ogni volta che conduciamo questo esperimento con due capriole, abbiamo una probabilità di avere testa a testa come risultato. Si noti che avremmo potuto fare questo problema anche con i decimali, per ottenere 0,5 volte 0,5 = 0,25.

Ecco il modello finale di domanda discusso in questo articolo: "Una moneta equa viene lanciata 20 volte di seguito. Quali sono le probabilità che atterrerà sulla testa ogni volta? Esprimi la tua risposta usando un esponente. " Come abbiamo visto prima, abbiamo a che fare con una condizione "e" per eventi indipendenti. Abbiamo bisogno del primo capovolgimento per essere teste, e il secondo capovolgimento per essere teste, e il terzo, ecc.

Dobbiamo calcolare 1/2 volte 1/2 volte 1/2, ripetuto un totale di 20 volte. Il modo più semplice di rappresentarlo è mostrato a sinistra. È (1/2) elevato alla ventesima potenza. L'esponente viene applicato sia al numeratore che al denominatore. Poiché 1 alla potenza di 20 è solo 1, potremmo anche scrivere la nostra risposta come 1 diviso per (2 alla ventesima potenza).

È interessante notare che le probabilità reali di accadere sopra sono circa uno su un milione. Anche se è improbabile che una persona in particolare ne faccia esperienza, se dovessi chiedere ad ogni singolo americano di condurre questo esperimento in modo onesto e accurato, un buon numero di persone segnalerebbe il successo.

Gli studenti dovrebbero assicurarsi che si trovano a proprio agio lavorando con i concetti di probabilità di base discussi in questo articolo, poiché vengono visualizzati abbastanza frequentemente.