Se hai seguito la copertura di March Madness di Sciencing, sai che statistiche e numeri giocano un ruolo importante nel Torneo NCAA.

La parte migliore? Non devi essere un fanatico dello sport per lavorare su alcuni problemi di matematica incentrati sullo sport.

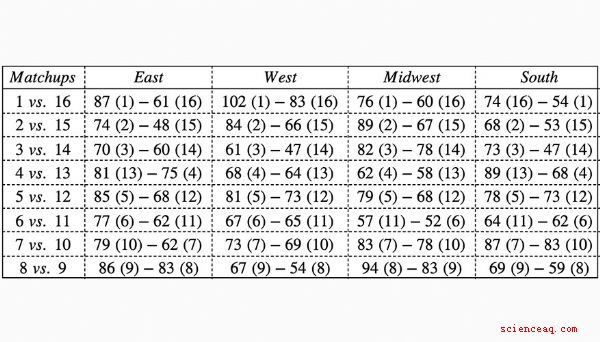
Abbiamo creato una serie di domande di matematica che incorporano i dati dei risultati di Madness dello scorso anno. La tabella seguente mostra i risultati di ogni Round di 64 matchup di seeding. Usalo per rispondere alle domande 1-5.

Se non vuoi vedere le risposte, torna alla scheda originale.

Buona fortuna!
Domande sulle statistiche:

Controlla i nostri articoli su media, mediana, modalità e intervallo interquartile se devi ripassare prima di iniziare.

Domanda 1: Qual è la differenza media dei punteggi in East, West, Midwest e South Region per il March Madness Round di 64 2018?

Domanda 2: Qual è la differenza mediana dei punteggi in East, West, Midwest e South Region per il March Madness Round di 64 del 2018?

Domanda 3: Qual è IQR (Interquartile Range) della differenza di punteggi in East, West, Midwest e South Region per il March Madness Round di 64 2018?

Domanda 4: Quali matchup sono stati outlier in termini della differenza di punteggi?

Domanda 5: Quale regione è stata più "competitiva" nel March Madness Round di 64 2018? Quale metrica useresti per rispondere a questa domanda: media o mediana? Perché?

Competitività:
Più piccola è la differenza tra vincere e perdere il punteggio, più "competitivo" è il gioco. Ad esempio: se i punteggi finali di due partite erano 80-70 e 65-60, secondo la nostra definizione quest'ultima partita era più "competitiva".
Statistiche Risposte:

Domanda 1 ( differenza di punteggi):

Est: 26, 26, 10, 6, 17, 15, 17, 3
Ovest: 19, 18, 14, 4, 8, 2, 4, 13
Midwest: 16, 22, 4, 4, 11, 5, 5, 11
Sud: 20, 15, 26, 21, 5, 2, 4, 10

Domanda 2 (media della differenza dei punteggi):

Media \u003d Somma di tutte le osservazioni /Numero di osservazioni
Est: (26 + 26 + 10 + 6 + 17 + 15 + 17 + 3 ) /8 \u003d 15
Ovest: (19 + 18 + 14 + 4 + 8 + 2 + 4 + 13) /8 \u003d 10.25
Midwest: (16 + 22 + 4 + 4 + 11 + 5 + 5 +11) /8 \u003d 9.75
Sud: (20 + 15 + 26 + 21 + 5 + 2 + 4 + 10) /8 \u003d 12.875

Domanda 2 (mediana della differenza dei punteggi ):

La mediana è il valore del 50 ° percentile.

La mediana di un elenco può essere trovata disponendo i numeri in ordine crescente e quindi selezionando il valore medio. Qui poiché il numero di valori è un numero pari (8), quindi la mediana sarà media dei due valori medi, in questo caso media del 4o e 5o valore.

Est: media di 15 e 17 \u003d 16
Ovest: media di 8 e 13 \u003d 10,5
Midwest: media di 5 e 11 \u003d 8
sud: media di 10 e 15 \u003d 12,5

Domanda 3 (IQR di differenza dei punteggi):

IQR è definito come la differenza tra il 75 ° percentile (Q3) e il 25 ° valore percentile (Q1).
\\ def \\ arraystretch {1.3} \\ begin {array} {