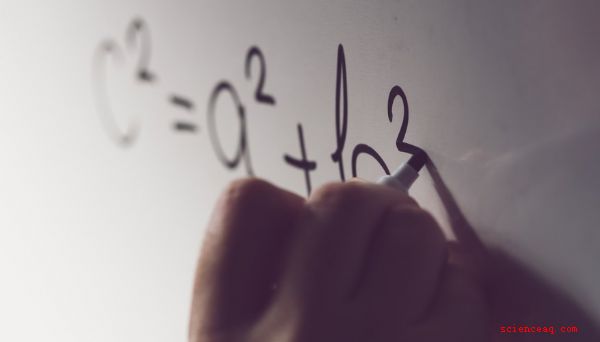
Una delle virtù della geometria, dal punto di vista dell'insegnante, è che è altamente visiva. Ad esempio, puoi prendere il Teorema di Pitagora - un elemento fondamentale della geometria - e applicarlo per costruire una spirale simile a una lumaca con un numero di proprietà interessanti. A volte chiamato spirale quadrata o spirale di Teodoro, questo mestiere ingannevolmente semplice dimostra relazioni matematiche in modo accattivante.
Una breve rassegna del teorema
Il teorema di Pitagora afferma che in un triangolo ad angolo retto , il quadrato dell'ipotenusa è uguale al quadrato degli altri due lati. Espresso matematicamente, significa A al quadrato + B al quadrato \u003d C al quadrato. Finché conosci i valori di due lati qualsiasi di un triangolo rettangolo, puoi utilizzare questo calcolo per arrivare a un valore per il terzo lato. L'unità di misura effettiva che si sceglie di utilizzare potrebbe essere qualsiasi cosa da pollici a miglia, ma la relazione rimane la stessa. È importante ricordare perché non lavorerai sempre necessariamente con una misurazione fisica specifica. Puoi definire una linea di qualsiasi lunghezza come "1" ai fini del calcolo e quindi esprimere ogni altra linea in base alla sua relazione con l'unità prescelta. Ecco come funziona la spirale.
Avvio della spirale
Per costruire una spirale, crea un angolo retto con i lati A e B di uguale lunghezza, che diventa il valore "1". Quindi, crea un altro triangolo rettangolo usando il lato C del tuo primo triangolo - l'ipotenusa - come lato A del nuovo triangolo. Mantenere il lato B della stessa lunghezza al valore scelto di 1. Ripetere nuovamente lo stesso processo, utilizzando l'ipotenusa del secondo triangolo come primo lato del nuovo triangolo. Ci vogliono 16 triangoli per arrivare fino al punto in cui la spirale inizierebbe a sovrapporsi al punto di partenza, che è dove l'antico matematico Teodoro si è fermato.
The Square Root Spiral
Il teorema di Pitagora ci dice che l'ipotenusa del primo triangolo deve essere la radice quadrata di 2, perché ogni lato ha un valore di 1 e 1 al quadrato è ancora 1. Pertanto ogni lato ha un'area di 1 al quadrato e quando vengono aggiunti, il risultato è 2 al quadrato. Ciò che rende interessante la spirale è che l'ipotenusa del triangolo successivo è la radice quadrata di 3, e quella successiva è la radice quadrata di 4, e così via. Questo è il motivo per cui viene spesso definita spirale quadrata, piuttosto che spirale pitagorica o spirale di Teodoro. In pratica, se hai intenzione di creare una spirale disegnando su carta o tagliando triangoli di carta e montandoli su un supporto di cartone, puoi calcolare in anticipo quanto può essere grande il tuo valore di 1 se la spirale finita è per adattarsi alla pagina. La linea più lunga sarà la radice quadrata di 17, per qualsiasi valore di 1 tu abbia scelto. Puoi lavorare a ritroso dalle dimensioni della tua pagina per trovare un valore adeguato di 1.
La spirale come strumento di insegnamento
La spirale ha un numero di usi in classe o impostazioni di tutoraggio, a seconda dell'età degli studenti e la loro familiarità con i fondamenti della geometria. Se stai solo introducendo i concetti di base, la creazione della spirale è un tutorial utile sul teorema di Pitagora. Ad esempio, potresti farli fare i calcoli in base a un valore di 1 e poi di nuovo usando una lunghezza del mondo reale in pollici o centimetri. La somiglianza della spirale con un guscio di lumaca offre l'opportunità di discutere su come si presentano le relazioni matematiche nel mondo naturale e - per i bambini più piccoli - si presta a schemi decorativi colorati. Per gli studenti avanzati, la spirale mostra una serie di relazioni intriganti mentre continua attraverso molteplici avvolgimenti.