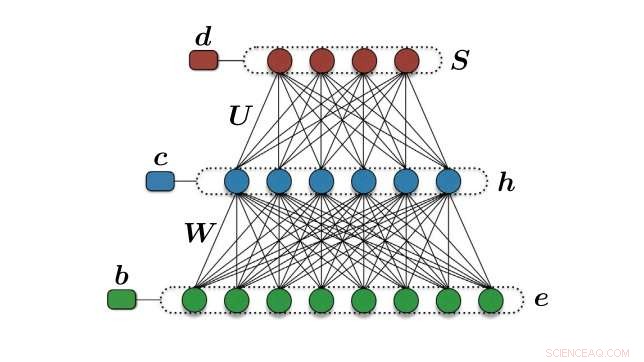
L'architettura del decodificatore neurale. Credito:Torlai et al. ©2017 American Physical Society
(Phys.org)—I fisici hanno applicato la capacità degli algoritmi di apprendimento automatico di apprendere dall'esperienza a una delle maggiori sfide che l'informatica quantistica deve affrontare attualmente:correzione degli errori quantistici, che viene utilizzato per progettare protocolli di calcolo quantistico tolleranti al rumore. In un nuovo studio, hanno dimostrato che un tipo di rete neurale chiamata macchina di Boltzmann può essere addestrata per modellare gli errori in un protocollo di calcolo quantistico e quindi ideare e implementare il metodo migliore per correggere gli errori.
I fisici, Giacomo Torlai e Roger G. Melko presso l'Università di Waterloo e il Perimeter Institute for Theoretical Physics, hanno pubblicato un articolo sul nuovo algoritmo di apprendimento automatico in un recente numero di Lettere di revisione fisica .
"L'idea alla base della decodifica neurale è quella di aggirare il processo di costruzione di un algoritmo di decodifica per la realizzazione di un codice specifico (date alcune approssimazioni sul rumore), e lascia che una rete neurale impari come eseguire il ripristino direttamente dai dati grezzi, ottenuto da semplici misurazioni sul codice, " Ha detto Torlai Phys.org . "Con i recenti progressi nelle tecnologie quantistiche e un'ondata di dispositivi quantistici che diventano disponibili a breve termine, decodificatori neurali saranno in grado di ospitare le diverse architetture, così come diverse fonti di rumore."
Come spiegano i ricercatori, una macchina di Boltzmann è uno dei tipi più semplici di reti neurali artificiali stocastiche, e può essere utilizzato per analizzare un'ampia varietà di dati. Le reti neurali in genere estraggono caratteristiche e modelli da dati grezzi, che in questo caso è un data set contenente i possibili errori che possono affliggere gli stati quantistici.
Una volta che il nuovo algoritmo, che i fisici chiamano decodificatore neurale, è addestrato su questi dati, è in grado di costruire un modello accurato della distribuzione di probabilità degli errori. Con queste informazioni, il decodificatore neurale può generare le opportune catene di errore che possono poi essere utilizzate per recuperare gli stati quantistici corretti.
I ricercatori hanno testato il decodificatore neurale su codici topologici quantistici comunemente usati nell'informatica quantistica, e dimostrato che l'algoritmo è relativamente semplice da implementare. Un altro vantaggio del nuovo algoritmo è che non dipende dalla geometria specifica, struttura, o dimensione dei dati, che gli permette di essere generalizzato a un'ampia varietà di problemi.
Nel futuro, i fisici intendono esplorare diversi modi per migliorare le prestazioni dell'algoritmo, ad esempio impilando più macchine Boltzmann una sopra l'altra per costruire una rete con una struttura più profonda. I ricercatori hanno anche in programma di applicare il decodificatore neurale a più complessi, codici realistici.
"Finora, i decodificatori neurali sono stati testati su semplici codici tipicamente utilizzati per benchmark, " Ha detto Torlai. "Una prima direzione sarebbe quella di eseguire la correzione degli errori sui codici per i quali non è ancora stato trovato un decodificatore efficiente, ad esempio i codici Low Density Parity Check. A lungo termine, credo che la decodifica neurale giocherà un ruolo importante quando si tratta di sistemi quantistici più grandi (centinaia di qubit). La capacità di comprimere oggetti ad alta dimensione in rappresentazioni a bassa dimensione, da cui deriva il successo del machine learning, consentirà di catturare fedelmente la complessa distribuzione che mette in relazione gli errori che si verificano nel sistema con gli esiti delle misurazioni."
© 2017 Phys.org