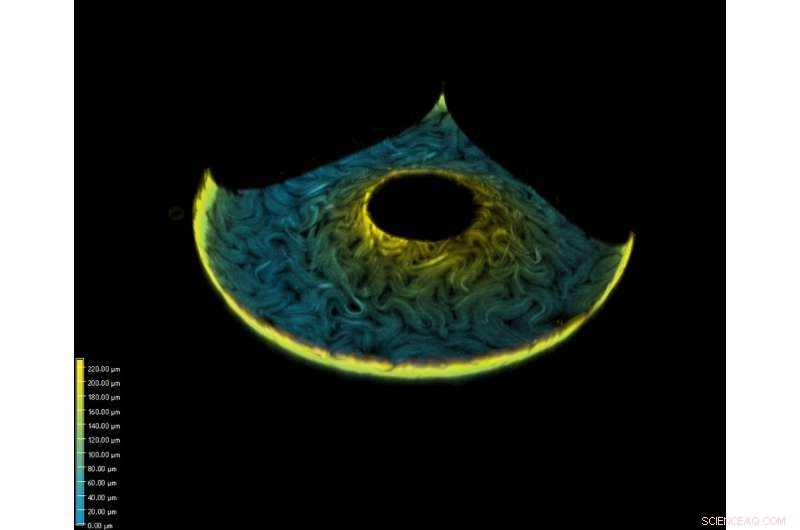
Immagine presa di un toroide utilizzando un microscopio confocale, falso colore per altezza. Le strutture vermiformi sono microtubuli guidati da proteine motorie chinesina. Credito:Perry Ellis, Georgia Tech
Immagina una minuscola gocciolina a forma di ciambella, ricoperti di vermi guizzanti. I vermi sono così fitti che devono allinearsi localmente l'uno rispetto all'altro. In questa situazione, diremmo che i vermi formano un cristallo liquido nematico, una fase ordinata simile ai materiali utilizzati in molti schermi piatti.
Però, la fase nematica formata dai vermi è piena di minuscole regioni in cui si perde l'allineamento locale - difetti nel materiale altrimenti allineato. Inoltre, perché i vermi si muovono costantemente e cambiano la loro configurazione, questa fase nematica è attiva e lontana dall'equilibrio.
In una ricerca riportata sulla rivista Fisica della natura , scienziati del Georgia Institute of Technology e dell'Università di Leiden nei Paesi Bassi hanno descritto i risultati di un esame teorico e sperimentale combinato di un tale nematico attivo sulla superficie di goccioline toroidali a forma di ciambella. Però, i ricercatori non hanno usato vermi veri, ma un nematico attivo composto da filamenti flessibili ricoperti da microscopici motori che convertono costantemente energia in movimento.
Questo particolare materiale attivo, originariamente sviluppato presso la Brandeis University, prende in prestito elementi del macchinario cellulare, con fasci di microtubuli astiformi che formano i filamenti, proteine motorie chinesina che agiscono come motori, e ATP come carburante. Quando questa attività è associata a difetti, i difetti "prendono vita, " muoversi come microrganismi che nuotano ed esplorare lo spazio - in questo caso, esplorando la superficie delle goccioline toroidali.
Studiando le goccioline toroidali coperte da questo nematico attivo, i ricercatori hanno confermato una previsione teorica di lunga data sui cristalli liquidi all'equilibrio, discusso per la prima volta da Bowick, Nelson e Travesset [Phys.Rev. E 69, 041102 (2004)] che i difetti nematici sulla superficie curva di tali goccioline saranno sensibili alla curvatura locale. Però, poiché il nematico attivo utilizzato in questo lavoro è lontano dall'equilibrio, i ricercatori hanno anche scoperto come l'attività interna cambiasse e arricchisse le aspettative.
"Ci sono state previsioni secondo cui i difetti sono molto sensibili allo spazio in cui abitano, specificatamente alla curvatura dello spazio, " ha detto Perry Ellis, uno studente laureato presso la Georgia Tech School of Physics e il primo autore del documento. "Il toro è un ottimo posto per indagare su questo perché l'esterno del toro, la parte che sembra localmente come una sfera, ha curvatura positiva mentre la parte interna di un toro, la parte che sembra una sella, ha curvatura negativa."
"La quantità che caratterizza un difetto è ciò che chiamiamo la sua carica topologica o numero di avvolgimento, " ha detto Alberto Fernandez-Nieves, un professore alla School of Physics della Georgia Tech e un altro dei coautori del documento. "Esprime come cambia la direzione di allineamento del cristallo liquido nematico mentre aggiriamo il difetto. Questa carica topologica è quantizzata, il che significa che può prendere solo valori da un insieme discreto che sono multipli della metà. "
In questi esperimenti, ogni difetto ha una carica topologica di +1/2 o -1/2. Per determinare l'addebito e l'ubicazione di ogni difetto, Ellis ha osservato le goccioline toroidali nel tempo utilizzando un microscopio confocale e quindi ha analizzato il video risultante utilizzando tecniche prese in prestito dalla visione artificiale. I ricercatori hanno scoperto che anche con i motori molecolari che portano il sistema fuori equilibrio, i difetti erano ancora in grado di percepire la curvatura, con i difetti +1/2 che migrano verso la regione di curvatura positiva e i difetti -1/2 che migrano verso la regione di curvatura negativa.
In questo nuovo lavoro, gli scienziati hanno fatto un passo avanti nella comprensione di come controllare e guidare i difetti in un materiale ordinato.
"Abbiamo imparato che possiamo controllare e guidare la materia attiva parzialmente ordinata usando la curvatura del substrato sottostante, " ha detto Fernandez-Nieves. "Questo lavoro apre opportunità per studiare come i difetti di questi materiali si dispongono su superfici che non hanno curvatura costante. Questo apre le porte al controllo della materia attiva usando la curvatura".
Una scoperta inaspettata dello studio è stata che il movimento costante dei difetti fa sì che la carica topologica media diventi continua, non assumendo più solo valori multipli della metà.
"Nel limite attivo dei nostri esperimenti, abbiamo scoperto che la carica topologica diventa una variabile continua che ora può assumere qualsiasi valore, " ha detto Fernandez-Nieves. "Questo ricorda ciò che accade a molti sistemi quantistici ad alta temperatura, dove il quanto, si perde la natura discreta degli stati accessibili e delle variabili associate.
Invece di essere caratterizzato da proprietà quantizzate, il sistema diventa caratterizzato da proprietà continue."
Le osservazioni di Ellis sulle goccioline si sono confrontate bene con quelle delle simulazioni numeriche fatte dall'assistente professore Luca Giomi e dal ricercatore post-dottorato Daniel Pearce presso l'Instituut-Lorentz for Theoretical Physics presso l'Universiteit Leiden nei Paesi Bassi.
"Il nostro modello teorico ci ha aiutato a decifrare i risultati sperimentali e a comprendere appieno il meccanismo fisico che governa il movimento dei difetti, "disse Pearce, "ma ci ha anche permesso di andare oltre le attuali prove sperimentali". Giomi ha aggiunto:"L'attività cambia la natura dell'interazione tra difetti e curvatura. Nei sistemi debolmente attivi, i difetti sono attratti da regioni di curvatura gaussiana dello stesso segno. Ma in sistemi fortemente attivi, questo effetto diventa meno rilevante e i difetti si comportano come camminatori casuali persistenti confinati in uno spazio chiuso e disomogeneo".
Ci sono molti esempi di sistemi attivi guidati da attività interne, compresi i microrganismi del nuoto, stormi di uccelli, sciami di robot e flussi di traffico. "I materiali attivi sono ovunque, quindi i nostri risultati non si limitano solo a questo sistema su un toro, " Ellis ha aggiunto. "Potresti vedere lo stesso comportamento in qualsiasi sistema attivo con difetti".
La ricerca pone le basi per lavori futuri sui fluidi attivi. "I nostri risultati introducono una nuova struttura per esplorare le proprietà meccaniche dei fluidi attivi e suggeriscono che la materia attiva parzialmente ordinata può essere guidata e controllata tramite gradienti nella geometria intrinseca del substrato sottostante, " hanno scritto gli autori in un riassunto del loro articolo.