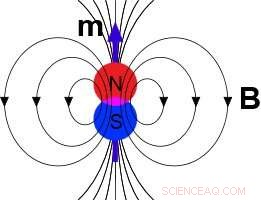
Gilbertiano:dipolo magnetico. Credito:en.wikipedia.org/wiki/Dipolo magnetico
I libri di testo attuali fanno spesso riferimento alla forza di Lorentz-Maxwell governata dalla carica elettrica. Ma raramente si riferiscono all'estensione di quella teoria richiesta per spiegare la forza magnetica su una particella puntiforme. Per le particelle elementari, come muoni o neutrini, la forza magnetica applicata a tali cariche è unica e immutabile. Però, a differenza della carica elettrica, la forza della forza magnetica non è quantizzata. Perché la forza magnetica agisca su di essi, il campo magnetico deve essere disomogeneo. Quindi questa forza è più difficile da comprendere nel contesto di particelle la cui velocità è vicina alla velocità della luce.
Inoltre, la nostra comprensione di come una particella puntiforme che trasporta una carica si muova in presenza di un campo magnetico disomogeneo si basava fino ad ora su due teorie che si credeva differissero. Il primo deriva dallo studio di William Gilbert sul magnetismo elementare nel XVI secolo, mentre il secondo si affida alle correnti elettriche di André-Marie Ampère. In un nuovo studio appena pubblicato su EPJ C, gli autori Johann Rafelski e colleghi dell'Università dell'Arizona, STATI UNITI D'AMERICA, è riuscito a risolvere questa ambiguità tra le forme di forza magnetica ameperiana e gilbertiana. La loro soluzione permette di caratterizzare l'interazione di particelle la cui velocità è prossima alla velocità della luce in presenza di campi elettromagnetici disomogenei.
Nel nuovo studio, gli autori presenti, per la prima volta, un'importante intuizione su come la non omogeneità del campo magnetico influisca sulla dinamica di spin delle particelle, chiamata precessione di spin. Nessun lavoro precedente ha riconosciuto la necessità di rendere la forma della coppia magnetica coerente con la forma della forza magnetica - la coppia è stata resa coerente solo con la forza di Lorentz-Maxwell.
Questo progresso consente di quantificare l'impatto della non omogeneità del campo sull'esperimento di precisione. Cerca di risolvere una discrepanza nella comprensione delle correzioni del campo quantistico al momento magnetico del muone, una particella elementare spesso chiamata "elettrone pesante".
Questi risultati possono essere applicati allo studio dei neutrini, aprendo la porta a regni oltre il modello standard della fisica delle particelle. Rafelski e colleghi mostrano che la forza magnetica può essere grande per le particelle la cui velocità è molto vicina alla velocità della luce.