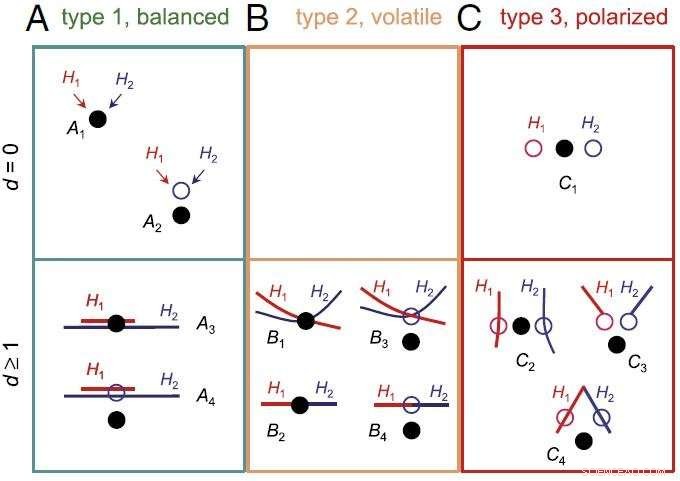
Classificazione dei problemi di selezione del modello bayesiano che coinvolgono due modelli ugualmente giusti o ugualmente sbagliati. Attestazione:ZHU Tianqi
Scienziati dell'University College London (UCL) e dell'Academy of Mathematics and Systems Science, Accademia cinese delle scienze (CAS, AMSS), hanno segnalato progressi nella comprensione dei problemi associati alla selezione del modello bayesiano. La ricerca suggerisce che il metodo bayesiano tende a produrre probabilità a posteriori molto elevate per gli alberi evolutivi stimati anche se gli alberi sono chiaramente sbagliati, e offre una possibile spiegazione di questo fenomeno.
Il confronto di modelli è ampiamente utilizzato in vari rami delle scienze in cui le ipotesi scientifiche sono formulate come modelli statistici e testate utilizzando dati osservati. Però, il confronto dei modelli è una questione spinosa sia nella statistica classica che nella statistica bayesiana.
Nella statistica classica, vengono confrontati due modelli annidati. Il framework non funziona quando i modelli confrontati non sono nidificati. In contrasto, La statistica bayesiana confronta diversi modelli calcolando le loro probabilità a posteriori, che indica la nostra fiducia o convinzione nel modello.
Non solo le due metodologie scaturiscono da filosofie drasticamente differenti, possono anche produrre conclusioni opposte nell'analisi degli stessi dati. È noto che la selezione del modello bayesiano converge al modello vero se il modello vero è incluso tra i modelli in esame.
Questo è, quando gli scienziati raccolgono più dati, la probabilità a posteriori per il modello giusto aumenterà e si avvicinerà al 100%, e saranno così sempre più certi di quale sia il vero modello.
Però, se tutti i modelli considerati sono sbagliati, il comportamento del metodo bayesiano è sconosciuto.
Gli scienziati hanno caratterizzato i problemi di selezione del modello bayesiano, e li ha classificati in tre tipi, ognuno dei quali mostra un comportamento diverso.
Nel caso scientificamente più interessante, cioè., quando i modelli confrontati sono distinti e quasi ugualmente errati, La selezione del modello bayesiano mostra un comportamento polarizzato problematico:tende a supportare un modello con tutta la sua forza in alcuni set di dati, ma supporta un altro modello in altri set di dati.
Il risultato può essere riassunto usando la seguente analogia:supponiamo che il mondo sia grigio, ma chiediamo a un saggio se è bianco o nero. Dà uno sguardo profondo al mondo e dice che è nero, con totale fiducia. Ma la prossima volta che faremo la stessa domanda, dice che è bianco, di nuovo con totale fiducia.
Questo studio è stato motivato da problemi di filogenetica molecolare, che è la scienza di elaborare le relazioni tra le specie utilizzando dati genetici, rappresentato da alberi evolutivi.
Questi diversi alberi si oppongono a modelli statistici nell'analisi bayesiana dei dati. I biologi evoluzionisti hanno a lungo osservato che il metodo tende a produrre probabilità a posteriori molto elevate per gli alberi evolutivi stimati (molto spesso il 100 percento), anche se gli alberi sono chiaramente sbagliati.
I nostri risultati forniscono una possibile spiegazione per questo comportamento spiacevole. Le implicazioni dei risultati per l'uso della selezione del modello bayesiano nella verifica di ipotesi scientifiche opposte in generale devono ancora essere esplorate.