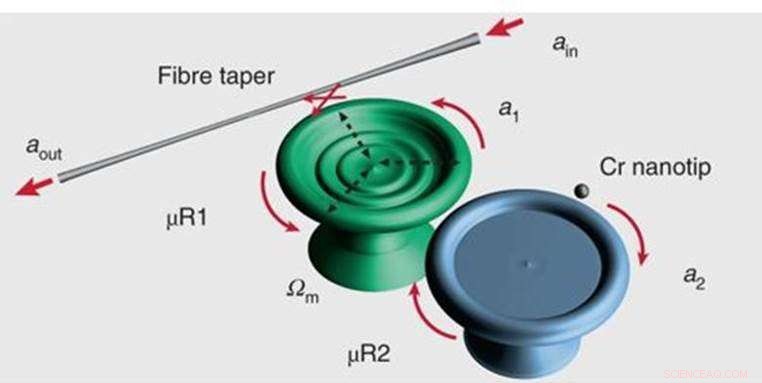
Schema schematico del laser fononico in un sistema risonatore composto:due risonatori microtoroidali µR1 (verde) e µR2 (blu), sono accoppiati tra loro da campi evanescenti. Il primo risonatore supporta una modalità ottica ad alto Q a1, e un modo meccanico con frequenza di risonanza m. Il secondo risonatore µR2, supporta una modalità ottica a basso Q a2, e il suo tasso di smorzamento è regolato da una nanopunta di silice rivestita di cromo che si avvicina a µR2. Credito: Fotonica della natura , nature.com/articles/s41566-018-0213-5
I quanti di base della luce (fotone) e del suono (fonone) sono particelle bosoniche che obbediscono in gran parte a regole simili e sono in generale ottimi analoghi l'uno dell'altro. I fisici hanno esplorato questa analogia in recenti indagini sperimentali su un laser fononico per fornire approfondimenti su una questione a lungo dibattuta su come un laser, o più specificamente, la sua larghezza della linea è influenzata quando viene utilizzata in un punto eccezionale (EP). I punti eccezionali sono singolarità nelle funzioni energetiche di un sistema fisico in cui due modalità di luce si uniscono (si combinano in una modalità) per produrre effetti insoliti. Fino a poco tempo fa, il concetto esisteva principalmente solo in teoria, ma ha ricevuto una rinnovata attenzione con dimostrazioni sperimentali in sistemi ottici come laser e strutture fotoniche. Gli studi sperimentali hanno coinvolto sistemi con simmetria parity-time per guadagno e perdita bilanciati di materiale, per garantire una forte intensità luminosa, immune alla retrodiffusione. Mentre i sistemi fisici chiusi e senza perdite sono descritti da operatori hermitiani in fisica quantistica, i sistemi con confini aperti che mostrano punti eccezionali (EP) non sono hermitiani.
Gli studi sperimentali dell'EP riguardano principalmente tali sistemi simmetrici parity-time che sfruttano abilmente l'interazione tra guadagno e perdita per abilitare funzionalità completamente nuove e inaspettate. In uno di questi salti concettuali, effetti ottici insoliti prodotti in questi sistemi hanno reso il mezzo invisibile in una direzione, un passo verso materiali ottici di nuova generazione con proprietà uniche mai viste con i materiali naturali. Tali concetti hanno avviato intensi sforzi di ricerca per esplorare i sistemi non hermitiani sia sperimentalmente che teoricamente.
Prima che il primo laser fosse dimostrato sperimentalmente, Schawlow e Townes calcolarono il limite quantistico fondamentale per la sua larghezza di riga; Gli EP sono storicamente associati all'estremo ampliamento della larghezza di linea del laser, oltre il limite fondamentale di Schawlow-Townes. Sebbene i modelli teorici abbiano fornito un quadro per calcolare la larghezza di linea del laser, non riescono a risolvere il problema direttamente al PE. Sperimentalmente, non è semplice dirigere un laser direttamente su un EP, poiché le modalità laser fotoniche diventano instabili vicino a un EP, causando laser caotici che potrebbero essere erroneamente percepiti come una linea laser estremamente ampia.
Ciò che accade realmente alla larghezza di riga quando un laser opera in corrispondenza di un EP è rimasto quindi finora poco chiaro. Comprendere i meccanismi responsabili dell'ampliamento della larghezza di linea consentirà alle risorse laser di nuove funzionalità a cui non avevamo accesso prima. Zhang et al., fornire una nuova elegante strategia per affrontare questo problema come pubblicato in Fotonica della natura , lavorando con un laser fononico piuttosto che con la sua controparte ottica (fotonica), osservarne il funzionamento in un momento eccezionale.
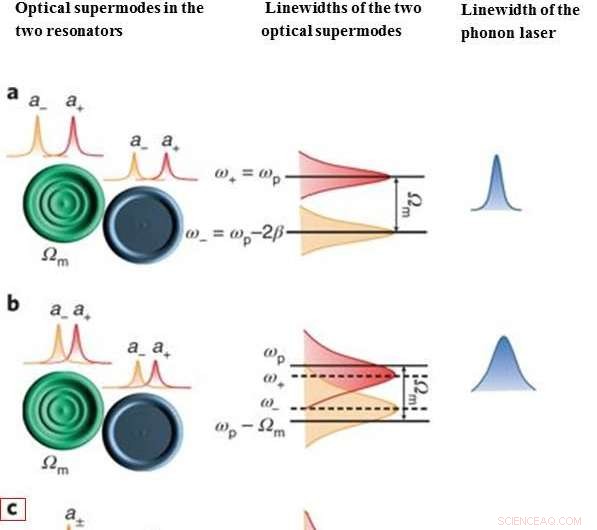
Sintonizzazione di un laser fononico su un punto eccezionale:la prima colonna è uno schema della distribuzione dei supermodi ottici a± nei due risonatori. La seconda colonna illustra la differenza di frequenza e le larghezze di riga dei due supermodi ottici a±. L'ultima colonna rappresenta la larghezza di riga del laser fononico. L'EP in cui i due supermodi ottici si fondono è a c, evidenziato in rosso. Il sistema transita da supermodi ottici ben separati e simmetricamente distribuiti a, B, a supermodi sempre più sovrapposti con sovrapposizione completa visti a c. Spinto dai modi ottici, il laser fononico eredita l'aumento del rumore ottico, riflesso da una larghezza di linea meccanica allargata (scatola rossa). Il regime dopo il PE si vede al d, e, spingendo il sistema lontano dall'EP portando al restringimento della larghezza di riga del laser fononico. Credito: Fotonica della natura , nature.com/articles/s41566-018-0213-5
Nello studio, i laser a fononi producono oscillazioni sonore coerenti (vibrazioni meccaniche) indotte dal pompaggio ottico, un concetto precedentemente sviluppato da Grudinin, Vahala e collaboratori, con caratteristiche tipiche dei laser a fotoni. Nel presente esperimento, i ricercatori hanno utilizzato un sistema optomeccanico simile con due microrisonatori in silice sussurro-modalità galleria (verde e blu). Il sistema fonone-laser composto è stato guidato verso o lontano dal suo EP per osservare il comportamento del laser a fononi vicino a un EP.
Per osservare l'allargamento della larghezza di riga, i fisici hanno eccitato otticamente la modalità meccanica del dispositivo sperimentale con la luce di un laser sintonizzabile accoppiato ad un singolo microrisonatore (verde) per mezzo di una fibra rastremata. Quindi, per guidare il sistema verso o lontano dal suo EP, hanno introdotto una perdita aggiuntiva al secondo microrisonatore (blu) utilizzando una punta in nanofibra di silice rivestita di cromo.
L'interazione tra guadagno e perdita è stata sfruttata in questo modo per sintonizzare un laser fononico su un EP. Il laser fononico è interpretato come un processo parametrico a tre onde in cui due onde sono ottiche e la terza onda è acustica o meccanica. Zhang et al. fornito prove sperimentali dirette per mostrare la completa sovrapposizione dei supermodi ottici a EP, e che il rumore ottico potenziato con EP può essere trasferito direttamente al rumore meccanico, che porta all'allargamento della larghezza di riga osservato nei laser a fononi.
I vantaggi pratici sono facili da comprendere:le onde sonore si propagano a una velocità di circa cinque ordini di grandezza inferiore alla velocità della luce, e la lunghezza d'onda del suono è quindi corrispondentemente più corta di quella della luce della stessa frequenza. Questa funzione può consentire un'elevata precisione, misurazioni e immagini non distruttive, così come ottenere un'alta concentrazione di energia con onde sonore focalizzate. Il presente lavoro apre nuove prospettive per il rapporto tra rumore e fisica non hermitiana, con potenziali applicazioni in campi correlati come le tecnologie di elaborazione del segnale. Il sistema può essere utilizzato come dispositivo fononico su chip analogo a dispositivi fotonici completamente integrati per l'elaborazione delle informazioni. Più interessante, la piattaforma studiata può ampliare le conoscenze sulla fisica non hermitiana consentendo il rilevamento e il controllo degli EP in sistemi a due o più livelli.
© 2018 Phys.org