Un materiale isolante appena identificato che utilizza i principi di simmetria alla base dei modelli di carta da parati può fornire una base per il calcolo quantistico, secondo un team internazionale di ricercatori. Questo campione di piombo di stronzio (Sr2Pb3) ha uno stato superficiale del cono di Dirac quadruplo, un set di quattro, stati di superficie elettronici bidimensionali che si allontanano da un punto nello spazio del momento in linee rette. Credito:Benjamin Wieder, Dipartimento di Fisica dell'Università di Princeton
Un team internazionale di scienziati ha scoperto un nuovo, forma esotica di materiale isolante con una superficie metallica che potrebbe consentire un'elettronica più efficiente o persino l'informatica quantistica. I ricercatori hanno sviluppato un nuovo metodo per analizzare i composti chimici esistenti che si basa sulle proprietà matematiche come la simmetria che governano i modelli ripetuti visti nella carta da parati di tutti i giorni.
"La bellezza della topologia è che si possono applicare i principi di simmetria per trovare e classificare i materiali, " ha detto B. Andrei Bernevig, professore di fisica a Princeton.
La ricerca, apparso il 20 luglio sulla rivista Scienza , prevedeva una collaborazione tra gruppi della Princeton University, l'Università della Pennsylvania (Penn), Università di Sungkyunkwan, Freie Universität Berlin e il Max Planck Institute of Microstructure Physics.
La scoperta di questa forma di piombo-stronzio (Sr 2 Pb 3 ) completa una ricerca decennale di un materiale tridimensionale sfuggente che combina le proprietà elettroniche uniche del grafene bidimensionale e degli isolanti topologici tridimensionali, una fase della materia scoperta nel 2005 in opere indipendenti di Charles Kane a Penn e Bernevig a Princeton.
Alcuni scienziati hanno teorizzato che gli isolanti topologici, che isolano al loro interno ma conducono elettricità sulla loro superficie, potrebbe servire come base per il calcolo quantistico super veloce.
"Puoi pensare a un isolante topologico come un bacio di Hershey, " ha detto Kane, un autore corrispondente sulla carta. "Il cioccolato è l'isolante e la lamina è un conduttore. Abbiamo cercato di identificare nuove classi di materiali in cui le simmetrie dei cristalli proteggono la superficie conduttiva. Quello che abbiamo fatto qui è identificare il tipo più semplice di isolante cristallino topologico. "
Il nuovo lavoro dimostra come le simmetrie di certe superfici bidimensionali, conosciuti come i 17 gruppi di carte da parati per i loro motivi simili a carte da parati, vincolare la disposizione spaziale (topologia) degli isolanti tridimensionali.
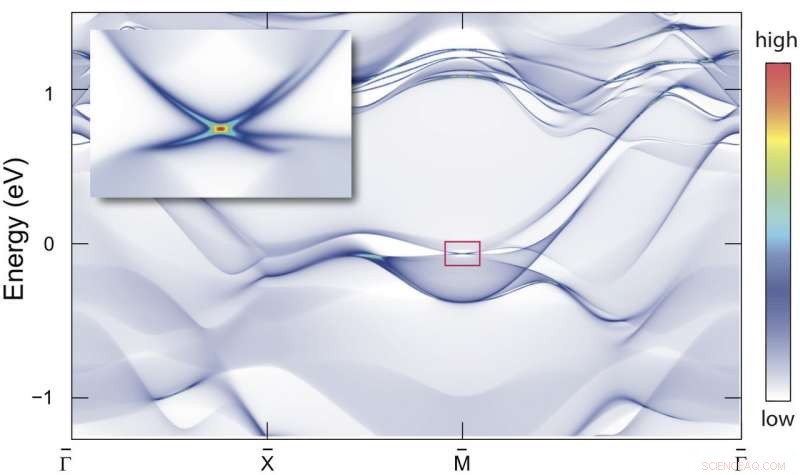
In un isolante topologico tridimensionale convenzionale, ogni superficie bidimensionale presenta un unico gruppo caratteristico di stati con dispersione a cono. Questi coni assomigliano agli elementi sul grafene chiamati coni di Dirac, caratteristiche che impregnano il materiale e altri semimetalli Dirac bidimensionali con le loro insolite qualità di trasporto elettronico, ma sono distinti perché il grafene possiede un totale di quattro coni di Dirac in due coppie che sono "incollati" insieme.
Kane aveva sospettato che con simmetrie di cristallo, un secondo tipo di isolante topologico potrebbe esistere con una singola coppia di coni di Dirac incollati. "Quello che ho capito è che una singola coppia di coni Dirac è impossibile in un materiale puramente bidimensionale, ma potrebbe essere possibile sulla superficie di un nuovo tipo di isolante topologico. Ma quando ho cercato di costruire un tale stato, i due coni venivano sempre scollati."
Una soluzione è emersa quando Benjamin Wieder, poi uno studente laureato nel gruppo di Kane e ora un associato post-dottorato di Princeton, ha visitato Princeton. A Princeton, Bernevig e il collega Zhi Jun Wang avevano appena scoperto "isolanti a clessidra" - isolanti topologici con strani schemi di stati a clessidra interconnessi - che Wieder ha riconosciuto agire come se avessi avvolto un cristallo tridimensionale con uno speciale tipo di carta da parati a motivi geometrici.
"Ci siamo resi conto che si poteva ottenere non solo l'isolante a clessidra, ma anche questo speciale isolante Dirac, trovando un cristallo che sembrava ricoperto dalla carta da parati giusta, ", ha detto Wieder.
In particolare, hanno riconosciuto che una coppia incollata di coni Dirac potrebbe essere stabilizzata su superfici di cristallo che hanno due linee intersecanti lungo le quali le superfici sembrano identiche dopo essere state capovolte e ruotate perpendicolarmente. Queste linee, noti come riflessi di scorrimento, caratterizzano i cosiddetti gruppi di carte da parati non simmorfiche, e fornire così l'omonimo di questa nuova fase, che il team ha soprannominato un "isolante Dirac non simmorfico".
I ricercatori si misero subito al lavoro applicando rigore matematico all'ispirazione di Wieder, con conseguente nuovo, carta da parati metodologia basata sulla simmetria per la diagnosi della topologia di massa dei cristalli tridimensionali.
"I principi di base sono abbastanza semplici che li abbiamo abbozzati sui tovaglioli quella sera stessa, " ha detto il co-autore Barry Bradlyn, ricercatore associato presso il Princeton Center for Theoretical Science (PCTS).
"Ma sono comunque abbastanza robusti da prevedere e comprendere uno zoo di nuove fasi topologiche in materiali reali, " ha detto Wang, assegnista di ricerca post-dottorato in fisica.
La scoperta ha permesso agli scienziati di mettere in relazione direttamente per la prima volta la simmetria di una superficie con la presenza degli stati superficiali topologici desiderati, ha detto Andrew Rappe di Penn, un altro co-autore sulla carta. "Ciò consente un mezzo elegante e immediatamente utile per progettare superfici desiderabili e stati dell'interfaccia".
Per identificare la fase isolante di Dirac in natura, i ricercatori hanno calcolato le strutture elettroniche di centinaia di composti precedentemente sintetizzati con superfici con due linee di scorrimento (gruppi di sfondi pgg e p4g) prima di identificare la nuova topologia in piombo-stronzio.
I chimici computazionali "sapevano che stavano cercando un ago in un pagliaio, ma nessuno si è preso la briga di dire loro quanto piccolo potrebbe essere l'ago, " ha detto Jennifer Cano, un ricercatore associato presso PCTS.
Man mano che vengono scoperti isolanti topologici ancora più esotici, il ruolo della simmetria del gruppo di sfondi, e dello speciale, coni simili al grafene nell'isolante di Dirac, sono stati ulteriormente solidificati.
"Quando puoi dividere un vero cono Dirac di superficie mantenendo la simmetria di inversione del tempo, succede qualcosa di veramente speciale, " ha detto Bernevig. "Si ottengono isolanti tridimensionali le cui superfici bidimensionali sono anche una sorta di isolante topologico." Tali fasi sono state previste recentemente nei cristalli di bismuto e ditelluride di molibdeno (MoTe2) da diversi membri della collaborazione.
Per di più, con l'uso di una nuova teoria, chimica quantistica topologica, i ricercatori sperano di trovare molte di più di queste fasi esotiche.
"Se potessimo dipingere questi materiali con la carta da parati giusta, vedremmo più isolanti Dirac, " disse Wieder, "ma a volte, anche lo sfondo sbagliato è interessante."