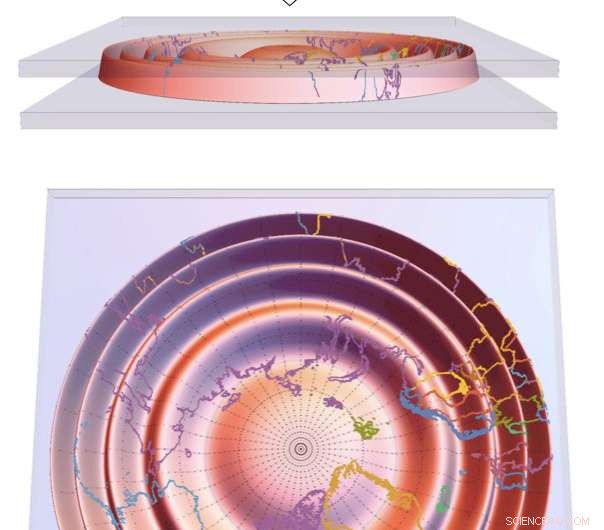
Questo schema mostra cosa succede quando un guscio elastico curvo, qui raffigurato come un globo, è costretto dal confinamento a cambiare da sferico a piatto. Se si raggrinzisce abbastanza, il guscio può appiattirsi quasi senza allungarsi. L'immagine in basso mostra che la distorsione della distanza introdotta quando si appiattisce un globo - rispetto a una mappa pre-schiacciata - può essere arbitrariamente più piccola man mano che il guscio diventa più sottile e più flessibile. Questa soluzione, sviluppato dai ricercatori di UMass Amherst, riconcilia principi fondamentali e apparentemente contraddittori della geometria e della meccanica. Credito:UMass Amherst/G. Grason
Affrontare un problema di fisica che risale a Galileo, tre ricercatori dell'Università del Massachusetts Amherst questa settimana propongono un nuovo approccio alla teoria di come i fogli sottili possono essere forzati a conformarsi a forme "geometricamente incompatibili"—pensate alla confezione regalo di un pallone da basket—che si basa sull'intreccio di due idee fondamentali di geometria e meccanica che a lungo si pensava fossero inconciliabili.
Il fisico teorico Benny Davidovitch, lo scienziato dei polimeri Greg Grason e il dottorando Yiwei Sun, scrivendo in Atti dell'Accademia Nazionale delle Scienze , suggerire e dimostrare tramite simulazioni numeriche che i fogli naturalmente piatti costretti a cambiare la loro curvatura possono adattarsi alla deformazione richiesta geometricamente sviluppando rughe microscopiche che piegano il foglio invece di allungarlo fino al punto di rottura, una soluzione che costa meno energia, anche.
Questo progresso è importante poiché i biotecnologi cercano sempre più di controllare il livello di deformazione riscontrato nei film sottili conformi a complessi, curve e forme tridimensionali del corpo umano, Per esempio, in sensori flessibili e indossabili per il monitoraggio della salute personalizzato, spiegano. Molti di questi dispositivi si basano sulle proprietà elettriche del film che si è dimostrato altamente vulnerabile allo stiramento, ma che può tollerare qualche piegatura.
Il nuovo concetto è uno di "abbastanza vicino, " Davidovitch dice:le non conformità che derivano dalla piegatura sono così piccole che in termini pratici, non costano quasi energia. "Offrendo strategie efficienti per gestire la tensione, prevederlo e controllarlo, offriamo un nuovo strumento quantitativo utile per le persone che prevedono le forze necessarie per goffrare o avvolgere fogli e gusci sottili nanoscopici su substrati di forme diverse, " affermano.
Aggiunge, "Il nostro lavoro mostra che consentendo piccole rughe nell'involucro, la quantità necessaria di stretching diminuisce drasticamente. Per un involucro estremamente sottile come oggi disponibile nei laboratori, lo stiramento può essere eliminato quasi del tutto."
Grason sottolinea, "Il nostro quadro teorico fornisce uno strumento semplice e adattabile per comprendere come controllare e manipolare, e idealmente per ottimizzare, il livello di deformazione che una data geometria impone a tale dispositivo, e quindi migliorare le sue prestazioni."
Davidovitch dice che ci sono due tipi di scienziati interessati a questo problema di vecchia data, uno meno motivato dalla praticità che dal modo in cui si applicano le leggi della Natura. Questi pensatori hanno familiarità con "il raggio di Galileo, "un problema di meccanica/fisica che immaginava una trave che sporgeva da un muro di pietra che si piegava o si deformava quando gli si aggiungeva del peso, lui nota. Prevedere le forze e la tensione su di esse ha rappresentato un enigma di vecchia data.
Galileo non ha risolto quanto si deformerà il raggio o come prevederlo, lui nota, ma questo problema relativo alla deformazione è stato successivamente esplorato e definito attraverso nuovi approcci alla geometria degli oggetti continui dal matematico e fisico tedesco Carl Friedrich Gauss. Fisici e matematici "hanno concentrato su di esso molta attività intellettuale nel corso dei secoli, "dice Davidovich.
Dopo Galilei, Davidovich dire, Il matematico svizzero Leonhard Euler sviluppò la "teoria dell'elastica, " che sostiene che gli oggetti confinati si piegano per evitare sforzi, questo è, qualsiasi variazione di lunghezza. Eulero dimostrò che una situazione in cui non avviene assolutamente alcuno stiramento può verificarsi in circostanze speciali, ma non nel tipo generale di confinamento definito dai vincoli geometrici di Gauss, Aggiunge.
Il nuovo strumento del team di UMass Amherst mostra, quando un vincolo non può essere perfettamente soddisfatto ma quasi soddisfatto, come trovare lo stato fisico o la forma che si adatta meglio. "È una nuova branca del calcolo variazionale, " dice Davidovitch. "Tutto quello che devo fare è ridurre al minimo la curvatura che elimina quasi tutto lo stiramento, e mi permette di trovare quello con la minor energia di flessione possibile."
Propongono un nuovo principio, l'elastica di Gauss-Eulero, che concilia i due cardini della meccanica classica e della geometria definiti in precedenza dai lavori di Eulero e Gauss. Invocano un nuovo regime di soluzioni delle complesse morfologie dei corpi sottili, un problema di intenso interesse recente dalla biofisica e dall'ingegneria dei materiali alla matematica applicata, sottolinea Grason.
Egli ricorda, "Quando abbiamo iniziato questa linea di ricerca, non immaginavamo come sarebbe andata a finire. Non stavamo cercando di risolvere questo problema." Ma il dottorando Sun, eseguire alcune simulazioni al computer, ha ottenuto risultati che hanno sfidato le ingenue ipotesi secondo cui il confinamento richiede più energia per allungarsi che per piegare il lenzuolo. Le formule che lui e Grason hanno proposto erano "impossibile, "Davikovic dice, "sembravano violare i teoremi geometrici fondamentali".
Sono rimasti bloccati per due anni, finché non si ricordarono del raggio di Galileo, quella che Davidovitch chiama una "contraddizione di pensiero, " che ha riformulato la domanda. È stato "molto soddisfacente" portare un nuovo strumento concettuale al problema che prima non era disponibile, lui dice. Grason aggiunge, "È fantastico avere una risposta al motivo per cui le nostre simulazioni iniziali si sono comportate in modo così strano, Certo. Ma alla fine ci porta a capire meglio la domanda, e come affronta una classe di problemi molto più ampia in un modo nuovo. Sì, questo ha una bella sensazione."