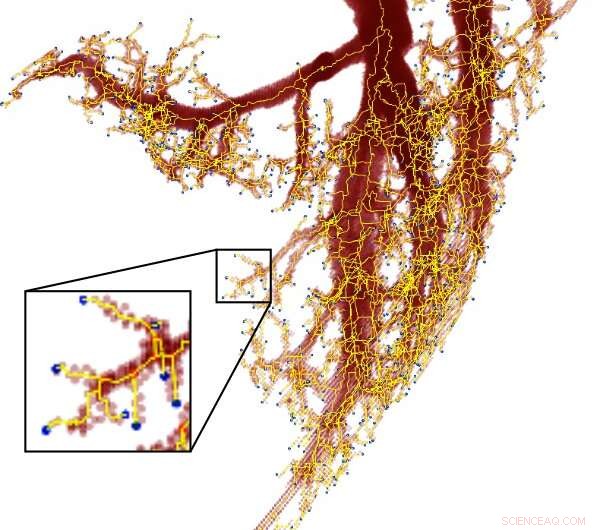
Poiché le vene si ramificano in divisioni approssimativamente proporzionate, sono anche considerati un frattale. Credito:immagine di cortesia/Mitchell Newberry
Potrebbero sembrare che i terremoti giganti e l'estrema ricchezza non abbiano molto in comune, ma la frequenza con cui il "Big One" colpirà San Francisco e la frequenza con cui qualcuno guadagnerà tanto denaro quanto Bill Gates possono essere entrambi previsti con una misurazione statistica chiamata esponente della legge di potenza.
Per il secolo scorso, i ricercatori hanno usato quella che viene chiamata legge di potenza per prevedere certi tipi di eventi, compresa la frequenza con cui si verificheranno i terremoti in determinati punti della scala Richter. Ma un ricercatore dell'Università del Michigan ha notato che questa legge sul potere non si adatta a tutte le circostanze.
Mitchell Newberry, un collega del Michigan e assistente professore presso l'UM Center for the Study of Complex Systems, suggerisce un adeguamento alla legge di potenza che tenga conto di eventi che aumentano o diminuiscono in proporzioni fisse, ad esempio, quando un manager guadagna circa il 20 percento in più del suo dipendente.
Questi aggiustamenti influenzano come stimare le probabilità di terremoti, il numero di capillari nel corpo umano, e le dimensioni delle megalopoli e dei brillamenti solari. E potrebbero rivedere quando aspettarsi il prossimo Big One.
Quando gli scienziati tracciano qualcosa come la probabilità di una ricchezza estrema su un grafico, la curva è una linea liscia. Questo perché le persone possono avere qualsiasi somma di denaro nei loro conti bancari.
"La morbidezza di questa curva significa che qualsiasi valore è possibile, " Disse Newberry. "Potrei guadagnare un centesimo in più con la stessa facilità di un centesimo in meno".
Questo non è esattamente il caso di eventi come i terremoti a causa del modo in cui vengono registrati sulla scala Richter. La magnitudo Richter dei terremoti aumenta o diminuisce con incrementi di 0,1, esponenzialmente. Un terremoto di magnitudo 3.1 è 1,26 volte più potente di un terremoto di magnitudo 3.0, quindi non tutti i valori sono possibili sulla scala. La scala Richter è un esempio di un concetto chiamato "auto-similarità, "o quando un evento o una cosa è fatta di copie proporzionalmente più piccole di se stesso.
Puoi vedere l'autosomiglianza in natura come la ramificazione delle vene in una foglia, o in geometria come triangoli adatti all'interno di triangoli più grandi della stessa forma, chiamato triangolo di Sierpinski. Così, per tenere conto di eventi che cambiano in proporzioni esatte, Newberry e il suo coautore Van Savage dell'Università della California, Los Angeles, costruito la legge di potenza discreta.

La curva di Koch si ripete all'infinito, mostrare auto-somiglianza. Credito:utente Wikimedia Leofun01
In queste equazioni della legge di potenza, l'esponente nell'equazione è la variabile per cui gli scienziati stanno risolvendo. Nei terremoti, quell'esponente, chiamato il valore b di Gutenberg-Richter, è stato misurato per la prima volta nel 1944 e indica la frequenza con cui è probabile che si verifichi un terremoto di una certa intensità. La legge sulla potenza discreta di Newberry ha prodotto una correzione dell'11,7% rispetto alle stime basate sulla legge sulla potenza continua, avvicinando l'esponente alla frequenza storica dei grandi terremoti. Anche una correzione del 5% si traduce in una differenza più che doppia di quando aspettarsi il prossimo terremoto gigante.
"Da 100 anni, la gente ha parlato più o meno di un tipo di distribuzione della legge sul potere. È la legge di potere, distribuzione della ricchezza e dei terremoti, " disse Newberry. "Solo ora, stiamo documentando queste scale discrete. Invece di una curva liscia, la nostra legge di potere sembra una scala infinita."
Newberry ha notato la falla nella legge di potenza continua nel suo studio della fisica del sistema circolatorio. Il sistema circolatorio inizia con un grande vaso sanguigno:l'aorta. Quando l'aorta si divide in diversi rami, le arterie carotidee e succlavia, ogni nuovo ramo diminuisce di diametro di circa due terzi.
Stava usando la legge di potenza continua per stimare le dimensioni dei vasi sanguigni mentre continuano a ramificarsi. Ma la legge sul potere ha prodotto dimensioni dei vasi sanguigni che non potevano verificarsi. Indicava che un vaso sanguigno poteva essere solo leggermente più piccolo del tronco da cui si diramava invece di circa due terzi delle dimensioni di quel tronco.
"Utilizzando la legge di potenza continua, stavamo solo ricevendo risposte che sapevamo essere sbagliate, " ha detto Newberry. "Eseguendo il debug di ciò che non è riuscito, abbiamo capito che questa distribuzione fa supporre che ogni dimensione dei vasi sanguigni sia ugualmente plausibile. Sappiamo che per una vera vascolarizzazione, non è così".
Quindi Newberry ha retroingegnerizzato la legge sul potere. Osservando i vasi sanguigni, Newberry potrebbe dedurre l'esponente della legge di potenza da due costanti:quanti rami ad ogni giunzione—due—e quanto è più piccolo ogni ramo rispetto al tronco. Misurare le dimensioni dei recipienti in ogni divisione, Newberry è stato in grado di risolvere per la distribuzione dei vasi sanguigni.
"C'è una via di mezzo tra una legge di potenza continua e la legge di potenza discreta, " Newberry ha detto. "Nella legge sul potere discreto, tutto è disposto in proporzioni perfettamente rigide dalla scala più alta all'infinitamente piccolo. Nella legge di potenza continua, tutto è disposto perfettamente in modo casuale. Quasi tutto ciò che è simile in realtà è un mix di questi due".
Lo studio di Newberry è pubblicato sulla rivista Lettere di revisione fisica .