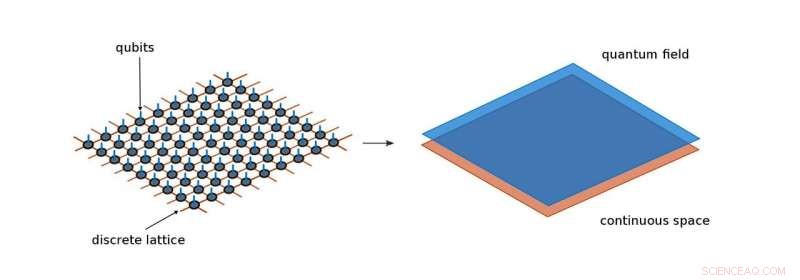
Gli stati della rete tensoriale standard descrivono i sistemi quantistici che vivono in uno spazio discreto, o reticolo, per esempio un array di qubit. Reti tensoriali continue, d'altra parte, ridurre le distanze reticolari fino a renderle infinitamente piccole e ripristinare così la continuità dello spazio. Per di qua, possono trattare i campi quantistici in modo più diretto. Credito:Istituto Max Planck di ottica quantistica
Calcolare accuratamente la dinamica di molte particelle quantistiche interagenti è un compito arduo. Esiste tuttavia un metodo di calcolo promettente per tali sistemi:reti tensoriali, che sono oggetto di ricerca nella divisione teoria presso il Max Planck Institute of Quantum Optics. L'obiettivo iniziale della rete tensoriale era sulle particelle quantistiche limitate a un reticolo, proprio come si verificano nei cristalli per esempio, o nei registri quantistici dei futuri computer quantistici. In un nuovo documento, il ricercatore post-dottorato Antoine Tilloy e il direttore della divisione di teoria Ignacio Cirac sono riusciti a estendere questo approccio al continuum. Un obiettivo a lungo termine è un elegante metodo di calcolo per le teorie quantistiche dei campi che descriva le forze fondamentali della fisica.
Descrivere i sistemi in cui molte particelle quantistiche interagiscono e producono collettivamente nuovi fenomeni è una delle sfide fondamentali della fisica. Un esempio di tale fenomeno quantistico a molti corpi è la superconduttività. La difficoltà è che le particelle si influenzano a vicenda. Di conseguenza, si possono derivare le equazioni della meccanica quantistica che descrivono questo comportamento collettivo, ma non risolto esattamente.
Nella meccanica quantistica, l'equazione dinamica deve catturare tutti i possibili stati in cui il sistema può trovarsi potenzialmente. E ce ne possono essere molti. Un esempio attualmente popolare in fisica sono i bit quantistici. Sono ottenuti ad esempio da elettroni appositamente preparati o atomi caricati elettricamente. Tali qubit hanno due stati opposti, che può assumere i valori zero e uno. Ma a differenza di un bit "classico", il qubit può anche essere localizzato in qualsiasi sovrapposizione di questi due stati. Se ora si accoppiano due qubit con una cosiddetta porta quantistica, lo spazio matematico astratto di tutti i possibili stati quantistici raddoppia. E ogni qubit aggiuntivo lo raddoppia di nuovo. I processori e le memorie dati dei computer convenzionali sono letteralmente invasi da questo numero esponenzialmente crescente di possibili stati quantistici. Anche i supercomputer falliscono dopo più di qualche dozzina di qubit. Solo computer quantistici, obbedire alle stesse regole della meccanica quantistica, sarà un giorno in grado di affrontare le dinamiche di sistemi quantistici più grandi.
Rendere calcolabile l'incalcolabile
L'esempio dei qubit si adatta, perché Ignacio Cirac ei suoi colleghi sono tra i pionieri di questo campo emergente della tecnologia dell'informazione quantistica. Il metodo delle "reti tensoriali, " che è l'oggetto di questo documento, deriva anche da questo campo di ricerca. Permette di ridurre abilmente lo spazio gigantesco di tutti i possibili stati quantistici di un sistema multiparticellare a una dimensione calcolabile. "Immagina tutti i possibili stati quantistici di un sistema a molte particelle come un'enorme area circolare, " spiega Antoine Tilloy. "Ma gli stati che sono veramente rilevanti per il nostro sistema rientrano in un cerchio molto più piccolo." L'arte ora sta nel trovare questo piccolo cerchio in uno spazio matematico astratto, ed è quello che possono fare le reti tensoriali.
Tilloy è un ricercatore post-dottorato nel gruppo di Cirac e insieme hanno appena pubblicato un articolo sulle reti tensoriali sulla rivista Revisione fisica X . Originariamente, i fisici li hanno applicati a matrici di singoli qubit. Le reti tensoriali si basavano quindi inizialmente su una griglia di oggetti matematici astratti, un po' come un filo di perle matematiche, vivere in posizioni discrete.
Le reti tensoriali si sono rivelate uno strumento di successo per eseguire calcoli per un'ampia classe di sistemi quantistici confinati alle griglie. Questo successo ha dato ai gruppi di ricerca teorici di tutto il mondo un'idea:questo metodo potrebbe essere applicato anche a sistemi fisici che non vivono sulle griglie, ma piuttosto nello spazio continuo? In breve, la risposta è si. Infatti, il metodo delle reti tensoriali può essere esteso al continuum e questo è quanto hanno dimostrato Tilloy e Cirac nel loro nuovo lavoro.
Nuovo strumento per le teorie quantistiche dei campi
Le cosiddette teorie quantistiche dei campi potrebbero essere un importante campo di applicazione per questa nuova cassetta degli attrezzi. Queste teorie costituiscono il fondamento della visione del mondo fisico di oggi. Descrivono accuratamente come funzionano tre delle quattro forze fondamentali della fisica secondo la meccanica quantistica. Queste forze sono mediate da particelle virtuali che esistono solo per il breve periodo di tempo necessario per trasmettere la loro forza.
Nella forza elettrica, Per esempio, le particelle mediatrici sono quanti di luce virtuali. "Questo rientra in ciò che è noto come elettrodinamica quantistica ed è ben compreso, " dice Tilloy. "Le cose si complicano con la cosiddetta cromodinamica quantistica." QCD, come viene brevemente chiamato, descrive le forze tra i quark, che a loro volta formano i mattoni dei nuclei atomici, i protoni e i neutroni. gluoni, "particelle adesive, " mediare la forza più forte in fisica. E questo "incolla" i quark insieme.
Ma a differenza dei fotoni virtuali, i gluoni possono anche influenzarsi fortemente a vicenda. Questa "autointerazione" porta allo spiacevole fatto che le equazioni della QCD possono essere risolte solo in casi limite, ad altissima energia. Per le energie inferiori, lo stato normale della materia nel nostro ambiente, questo non è possibile. Per questa ragione, i fisici finora devono lavorare con soluzioni approssimate. Il passaggio standard qui è quello di scomporre il continuum in una griglia artificiale di punti per la quale un potente computer può quindi calcolare soluzioni approssimate.
"Questo passaggio di discretizzazione è complesso, " dice Tilloy. Inoltre, tali semplificazioni hanno sempre lo svantaggio di rompere una fondamentale simmetria della natura quando si divide il continuum in una griglia di punti discreti. Sono quindi costretti ad allontanarsi dalla fisica reale. Il metodo delle reti tensoriali continue potrebbe fornire un aiuto qui, perché non richiede questa discretizzazione preventiva dello spazio. Forse un giorno si capirà il comportamento di quark e gluoni a basse energie. Oggi è ancora un problema aperto, ma le reti di tensori continue scoperte di recente potrebbero già essere parte della soluzione.