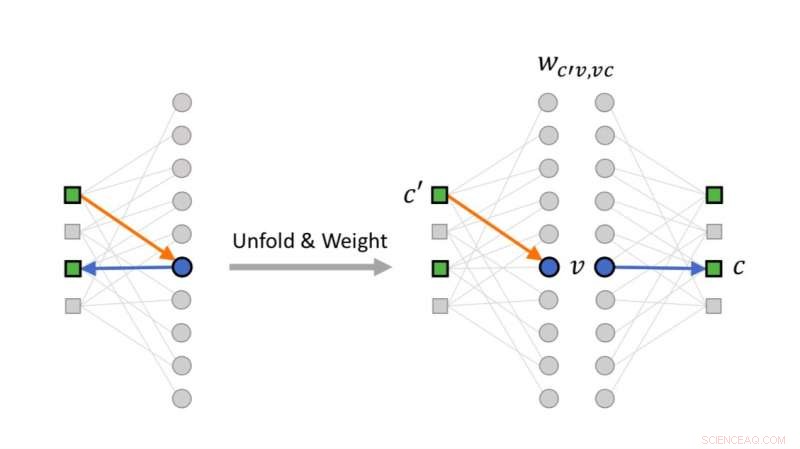
Propagazione delle credenze neurali come passaggio di messaggi spiegato e ponderato. Credito:Liu &Poulin.
Due ricercatori dell'Université de Sherbrooke, in Canada, hanno recentemente sviluppato e addestrato decodificatori di propagazione delle credenze neurali (BP) per codici quantistici di controllo di parità a bassa densità (LDPC). Il loro studio, delineato in un articolo pubblicato su Physical Review Letters, suggerisce che la formazione può migliorare significativamente le prestazioni dei decodificatori BP, aiutando a risolvere i problemi che sono comunemente associati alla loro applicazione nella ricerca quantistica.
"Dieci anni fa, Ho scritto un articolo con Yeojin Chung spiegando come gli algoritmi di decodifica standard per i codici LDPC, che sono ampiamente utilizzati nella comunicazione classica, fallirebbe nell'impostazione quantistica, "Davide Poulin, uno dei ricercatori che ha condotto lo studio, ha detto a Phys.org. "Questo problema mi ha ossessionato da allora. Di recente, le persone hanno iniziato a studiare l'uso delle reti neurali per decodificare i codici quantistici, ma tutti si sono concentrati su un problema (la decodifica dei codici topologici) che aveva già una serie di buone soluzioni progettate dall'uomo. Questa è stata l'occasione perfetta per rivisitare il mio problema aperto preferito e utilizzare le reti neurali per decodificare codici quantistici che non avevano un decoder precedentemente noto".
Mentre i decodificatori BP sono comunemente applicati in una varietà di impostazioni, finora si sono dimostrati inadatti alla decodifica di codici quantistici di correzione degli errori. Ciò è dovuto a una caratteristica quantistica unica denominata "degenerazione dell'errore, " il che significa essenzialmente che ci sono diversi modi per correggere un errore nelle impostazioni quantistiche.
Gli algoritmi BP classici sono costituiti da tre semplici equazioni. La struttura di queste equazioni consente una mappatura esatta su una rete neurale feed-forward. In altre parole, è possibile reinterpretare le equazioni BP comunemente usate per decodificare i codici LDPC come descrivere l'impostazione iniziale di una rete neurale.
La ricerca passata ha scoperto che questa "rete neurale iniziale" non funziona bene in ambienti quantistici, nonostante ottenga prestazioni migliori rispetto alle reti neurali casuali. Nel loro studio, Poulin e il suo collega Ye-Hua Liu hanno migliorato le prestazioni della "rete neurale iniziale" addestrandola con dati generati da simulazioni numeriche.
"L'addestramento è guidato da una funzione target che tiene conto degli effetti quantistici, " Liu ha detto a Phys.org. "In generale, i decodificatori neurali hanno il vantaggio di adattarsi a statistiche di rumore arbitrarie in canali realistici. In aggiunta a ciò, il nostro metodo è applicabile a codici LDPC quantistici senza strutture reticolari regolari. Questi codici sono molto promettenti per realizzare la correzione degli errori quantistici a basso costo".
I ricercatori hanno scoperto che l'addestramento dei decodificatori BP neurali utilizzando la tecnica adottata ha migliorato le loro prestazioni, per tutte le famiglie di codici LDPC testati. Inoltre, la tecnica di addestramento che hanno usato potrebbe aiutare a risolvere il problema della degenerazione che generalmente affligge la decodifica dei codici LDPC quantistici.
"L'addestramento della rete neurale BP può migliorare significativamente le sue prestazioni per la correzione degli errori quantistici, il che significa che un algoritmo classico può essere adattato all'ambiente quantistico mediante metodi di deep learning, " Liu ha detto. "Questo ci ispira a cercare altri esempi come questo nella fisica quantistica, per rivelare una connessione più ampia tra apprendimento profondo e scienze naturali. Ad esempio, la propagazione delle credenze è ampiamente utilizzata in molte altre aree di ricerca, compresa la fisica statistica, il che implica che la BP neurale potrebbe anche avvantaggiare la ricerca nella fisica statistica quantistica".
Nel loro lavoro futuro, Poulin e Liu intendono studiare la PA neurale nel contesto della fisica statistica. Se allenato con la stessa tecnica, i ricercatori si aspettano che BP, che viene anche chiamato "metodo della cavità" in questa particolare impostazione, mostrerà un miglioramento delle prestazioni anche in questo contesto.
"Più in generale, la propagazione delle credenze appartiene all'importante classe degli algoritmi di passaggio dei messaggi, che risulta essere strettamente correlato alle reti convoluzionali di grafi nella ricerca di deep learning, Liu ha aggiunto. "Sarebbe molto fruttuoso acquisire informazioni su queste strutture dal punto di vista di un fisico".
© 2019 Science X Network